Analysis and critique of the 100% WWS Plan
advanced by The Solutions Project
Analysis and critique of the 100% WWS Plan
advanced by The Solutions Project

Our overbuild factor relative to maximum seasonal demand, not relative to average demand, is 1.52. That's the ratio of our maximum annual energy production capability (“peak capacity”) to our nationwide maximum demand during August when air-conditioners are working hard. August’s seasonal maximum power demand is about 768 GW.61 So the factor now is 1167 GW ÷ 768 GW = 1.52.
The 100% WWS Plan can perhaps help with the seasonal maximum demand problem by the practice of demand management, usually called demand response - DR. For example, by shifting some daytime air-conditioning demand into the night, using chilled water and futuristic phase-change material technologies. DR can't shift between seasons of course, but it can shift between hours, thereby making August’s day-time demand not so peaky.
The author has no mathematical modeling tool at his disposal, so must be reduced to a seat-of-the-pants estimate of the necessary overbuild factor for an all-electric society energized mostly by unreliable sources.
It seems to me the intermittency issue by itself would require our present 2.5 X overbuild factor to be boosted to some value between 3 X and 4 X. Changing from 1080 GW of always-on power to only 68 GW of always-on power gives me shudders. (In Table 2, rows 4 and 5, geo + hydro = 4.26% of 1591 GW =
67.8 GW). But I'll swallow hard and place my bet on 3 X overbuild, as sufficient to cope with drastic reduction of always-on electric sources.
Then comes the matter of 100% of primary energy going to feeding the electric grid, not merely 39% as today. This proportional expansion by a factor of about 2.5 probably doesn't require another factor-of-2.5 increase in the already-greater overbuild from the previous paragraph. (Remember though, that it does require a substantial increase in absolute production capability, “peak capacity”, from 1167 GW in 2015 to 1591 GW in 2050, per the Plan.)
As described above, DR can accomplish intra-day hourly shifting among sectors' demands. For example, it can guarantee charging EV batteries only at night, and accessing commercial refrigeration facilities mostly at night (maybe lots of midnight-shift job openings in the food-distribution industry). It can shift into night-time the process of water-chilling for use as the next day's air-conditioning; and other demand-response management activities via the internet of things.
So one might guess that the additional factor of increase in overbuild can be just 1.2 X or 1.5 X. That is to say, the 3 X overbuild factor contingent on intermittency of fuel sources, stated in an earlier paragraph, must itself be boosted by another factor of 1.2 X or 1.5 X. Thereby giving us an overall overbuild factor of 3.6 X to 4.5 X.
Let that be my offer. For talking /disputation purposes, I will call it 4 X.
Hear ye, all environmentalists of weak faith in computer modeling 35 years into the future anticipating unproved technologies. Join with me in arguing that 1591 GW of production capability is grossly insufficient. Instead we would need 4 X 1591 GW = 6364 GW of production capability, in order to run the whole USA on a fossil-free and nuclear-free regime.
Ouch! That overall $15.2 trillion construction cost that we were bandying about? It's really 4 X $15.2 T = about 60 trillion dollars.
That 67,500 km2 for utility-scale PV solar? It's really 4 X 67,500 km2 =
262,800 km2 (101,500 sq mi). In other words, almost all of Arizona.
Onshore wind? Better not to ask. (Hint: Thank our stars for Thomas Jefferson. His 1803 Louisiana Purchase makes a nice dent in the reckoning.)
Another Course of Action - Nuclear
Of course we can't consider committing such wreckage upon our ecosystems and landscapes. It would be an ecocidal maniac who would really begin working toward a goal of 6364 GW, under the justification of "preserving the American way of life", or such nonsense. It would be hardly worth living at all, let alone "the American way”, if the only way were to defile our lovely land with 6364 gigawatts worth of windmills and solar panels.
But do acknowledge that the 100% WWS Plan points the way to reducing our society’s PRI-NRG consumption to just 1591 GW-y /year, down from 2010’s 3261 GW-y.51 Let us be appreciative to the Plan’s authors for urging us to aspire to that 1591-GW goal through 100% electrification of all energy sectors with elimination of all fossil fuels. On that score they deserve "A" for effort.
Our objection to the Plan isn't their societal /ecological goal. It's the klutzy method they have chosen to pursue that goal. Namely the land-hogging, material-intensive, GHG-emitting, expensive, diffuse-energy, low-density sources they’re using for their solution. Why such klutziness, when we have available to us a compact-size, low-material, low-CO2, concentrated energy, high-density energy source like nuclear fission?
Nuclear Generation 3+ technology, under construction right now and typified by the Westinghouse /Toshiba model AP1000 pressurized water reactor, can achieve the Plan’s 1591 GWavg of national PRI NRG a lot more elegantly. Meaning a lot less material, a lot less occupied land, and a lot less money.
And because it's always-on nature is even more definite than fossil combustion, Generation 3+ nuclear won't require 3 or 4 X overbuild factor. We can probably maintain the 2.5 X overbuild factor that works satisfactorily for us now with our old-fashioned fossil technologies.
Moreover, if we do eventually change our electricity structure to a more distributed model, with smaller generation plants more widely distributed, we can then almost certainly reduce our overbuild factor to less than 2.5 X.
Generation 3+ small modular reactors - SMRs - are just around the corner. They will have the same passive-cooling and safety features as the 1100-mega- watt model AP1000. SMR development is tending toward 250-megawatt capacity,62 so their land footprints will be only a fraction of the AP1000's footprint, which is itself less than 200 by 200 meters - 10 football fields.
SMRs’ very small footprint will allow them to be dispersed to individual neighborhoods, adjacent to the loads that they serve. Such a distributed-power electricity system is expected to be naturally more stable and reliable than the 20th-century concentrated-power electric grid model that drove the overbuild factor as high as 2.5 X to begin with.
But before we look forward to those happy days, let us examine the presently available AP1000 reactor, with regard to its land-use, material consumption, and money cost.
The Model AP1000 Pressurized Water Reactor:
Land, Material and Money
Land and material for an AP1000 are cut-and-dried. One reactor site (not counting the surrounding security zone) occupies less than 0.04 km2 (200 X 200 meters); the structure uses 15,500 tonnes of steel and 248,000 tonnes of concrete for its construction.63
AP1000’s cost is an article of contention. The Vogtle Georgia site where two such reactors are to be built is priced at $14 billion, giving a $7 billion
per-reactor cost.
But the Sanmen China site 150 miles from Shanghai has two model AP1000 units nearing completion, one in 2016 and the second in 2017. China National Nuclear Corporation - CNNC - will not commit to an estimate of Sanmen’s completed cost. But CNNC’s own proprietary design of Generation 3+ pressurized water reactor, a smaller 650-MW unit, has been finished and is generating power now. It’s located on Hainan Island, 300 miles from Hong Kong in the Tonkin Gulf, alongside another identical unit scheduled on-line in 2017.
With combined capacity of 1300 MW, the pair have expected completed cost of $3.15 billion.64 Normalized to an 1120-MW AP1000, that’s equivalent to one large reactor costing $2.7 billion. [1120 MW ÷ 1300 MW X $3.15 B = $2.7 B]
The 100% WWS Plan’s Table S14 on page 91 cites several cost studies that range from $5583 /kW to $6640 /kW in the near-term for advanced pressurized water reactors - APWR - like the AP1000. Future-cost studies on page 92 project $3800 to $6511 /kW.
The cost figures have a wide spread, as usual. For discussion we will set aside the low China figure, though their low price is corroborated by South Korea’s experience at about $1700 /kW (accepting the official currency exchange) for a similar Gen 3 reactor,65 suggesting just $1.9 billion for an AP1000-size unit.
But current evidence of Korean nuclear technical /industrial expertise is the United Arab Emirates project now being built by Korea Electric Power Co - KEPCO. That project involves four of the KEPCO-designed model APR-1400 reactors, for a reported price of $20.4–$25 billion. 65 .5 The first of its four reactors is nearly complete, scheduled to start up in 2017.
Normalized to the 1120-MW AP1000 reactor, KEPCO’s UAE bid cost (assuming midrange price of $22.7 billion) is $4.5 billion per reactor.
[4 X 1400 MWp = 5600 MWp; $22.7 B ÷ 5600 MWp = $4.05 /Wp; $4.05 X 1120 MWp = $4.5 B per AP1000 reactor]
In the interest of non-impeachability, we will simply average all eight of the American near-term and future costs published by the Plan, giving $5532 /kW as our working figure.66 Going forward to 2050 then, expect AP1000s to average $6.2 billion. [1120 MW X $5532 /kW = $6.2 B]
The Gen 3+ design requires less frequent fuel changes than older-design reactors, enabling the AP1000 to perform at 93% CF.67 Its average power will be 1120 MWp X 0.93 = 1040 MWavg.
The 100% WWS Plan’s goal of 1591 GWavg PRI NRG could thus be achiev-ed by 1530 reactors acting alone. [1591 GWavg ÷ 1040 MWavg = 1530]
However, our already installed wind, hydro and solar capacity can supply a small portion of that demand. In 2015 their contributions were:
Wind: 21.8 GW-y67.3(4.7% of 2015’s electric demand)
Hydro: 28.7 GW-y67.5(6.2% of 2015’s electric demand)
Solar: 4.6 GW-y67.7(1.0% of 2015’s electric demand)
Total WWS: 55.1GW-y (11.9% of 2015’s electric demand)
With WWS making its small contribution the nuclear fleet would need to supply only 1591 – 55.1 = 1536 GWavg.
There is one final consideration regarding the Plan It proposes to use 11.48% of its grid power, 182.6 GW, to produce elemental hydrogen by electrolyzing fresh water.67.8 The hydrogen is intended for two applications:
1) Combustion with oxygen to attain very high temperatures, above 1000 deg C, for certain industrial processes. About 23% of hydrogen production is intended for this purpose, consuming 41.0 GW of grid power.
2) Fuel-cell electric vehicles for heavy transportation. About 77% of hydrogen production is so intended, consuming 141.4 GW of grid power.67.9 Presumably the Plan’s authors assess the U.S. trucking industry as competent to safely manage hydrogen tanks on their fleets. The general automobile-driving public does not qualify of course.
Process heat application 1) is justified. Generation 3+ Advanced Passive reactors cannot achieve temperatures in that range. So even though water electrolysis for hydrogen results in a large portion of the 41.0 GW grid demand being wasted as heat, that is unavoidable.
Figure C
Fuel-cell transport 2) is quite inefficient, with the water electrolyzer /fuel-cell combination in Figure C showing only 25.6% electric-to-electric conversion efficiency. That is to say, of the 141.4 GW grid load, only 25.6%, or 36.2 GW actually reaches the drive motors that propel the trucks. The other 74.4%, or 105.2 GW, is emitted as waste heat into the environment. By replacing fuel cells with batteries for electric vehicle trucking the all-nuclear grid reduces its power demand by that 105 GW wasted amount.
Thus the nuclear demand of 1536 GW after WWS contribution can be further reduced to 1431 GWavg. [1536 GW – 105 GW = 1431 GW]
Therefore only 1376 reactors are required. [1431 GWavg ÷ 1040 MWavg = 1376]
Money:
At $6.2 billion per reactor, multiplied by 1376 reactors, the nuclear path would cost $8.5 trillion. Gen 3+ Advanced Passive nuclear
Which is quite a better deal than the $15-or-so trillion figure that jumped out at us for a WWS build-out.
It must be acknowledged that building 1376 reactors in 35 years is a daunting task. It would mean 39 reactors per year, which far exceeds France’s
3.7 reactors per year built between 1973 and 1988. Their 15-year performance has been the world’s most productive nuclear build-out. On the other hand, US GDP is about 7 X greater than France’s.
The recently published China five-year plan envisions building 7 new reactors each year from 2015 to 2030.68 So it may be that 39 reactors per year for America in unrealistic. Well, 35 years is just an aspiration. Even if it takes
70 years, the thing is to get started.
In order to make comparisons of material, CO2 and land, we now summarize for the nuclear choice:
Gen 3+ Nuclear Plan
Steel: 1376 reactors X 15,500 tonnes steel = 21.3 million tonnes steel
Concrete: 1376 X 248,000 tonnes concrete = 341 million tonnes concrete
CO2: 21.3 M t X 1.8 t + 341 M t X 1.2 t = 448 million tonnes CO2
Land: 1376 X 0.04 km2 = 55 km2 (21 sq mi, less than Manhattan island).*
Money: 1376 reactors X $6.2 B = $8.5 trillion Gen 3+ Advanced Passive nuclear
*For the foreseeable future, large reactors will be surrounded by security zones until technology evolves to permit underground placement of Small Modular Reactors - SMRs. So the reserved site area for an AP1000 will be much larger than 0.04 km2. For discussion purposes let us assume one-half square mile (1.3 km2) as fenced security zone area. Then the amount of occupied land throughout the US would be 1376 X 1.3 km2 = 1790 km2 (690 sq mi). That’s about half of Long Island, New York.
We will now compare these values to the 100% WWS Plan’s entire build-out, with use-values extracted from our previous sections.
Comparison of 100% WWS Plan to
Gen 3+ Nuclear Plan
Steel:
Utility PV: 186 M tonnes
Residential PV: 6.5 M t (aluminum)
Commercial PV: 44 M t
CSP: 188 M t
Onshore wind: 188 M t
Offshore wind: 180 M t
Total Steel: 793 million tonnes 100% WWS Plan, entire
Concrete:
Utility PV: negligible
Residential PV: none
Commercial PV: none
Onshore wind: 701 M t
Offshore wind: 673 M t
CSP: 605 M t
Total Concrete: 1979 million tonnes 100% WWS Plan, entire
CO2:
Utility PV: 11,400 M t CO2eq
Residential PV: 2300 M t CO2eq
Commercial PV: 1700 M t CO2eq
Onshore wind: 885 M t
Offshore wind: 1133 M t
CSP: 1060 M t
Total CO2eq: 18,500 million tonnes 100% WWS Plan, entire
About 2.7 years of our BAU emissions.36
Land:
Utility PV: 67,500 km2 {perhaps less, per NREL’s packing factor approach in future}
Residential PV: none
Commercial PV: none
Onshore wind: 289,200 km2
Offshore wind: 69,500 km2 (ocean)
CSP: 19,200 km2
Total Land: 375,900 km2 (145,100 sq mi)
{perhaps less, per NREL’s packing factor approach in future}
86,700 km2 is unusable for agriculture or any other purpose.
That’s 1.1% of the lower 48 states. 100% WWS Plan, entire
Ocean: 69,500 km2 (26,800 sq mi)100% WWS Plan, entire
Money:
Utility PV: $5.3 T
Residential PV: $1.5 T
Commercial PV: $0.9 T
Onshore wind: $2.6 T
Offshore wind: $2.7 T
CSP: $2.2 T
Total Money: $15.2 trillion 100% WWS Plan, entire
(Or $25.9 trillion per the Plan’s Table S14 sources.)
Factor of difference Percentage
WWS ÷ nuclear nuclear ÷ WWS
Steel: 793 ÷ 21.3 = 37.2 X 21.3 ÷ 793 = 2.7%
Concrete: 1979 ÷ 341 = 5.8 X 341 ÷ 1979 = 17.2%
CO2eq: 18,500 ÷ 448 = 41.3 X 448 ÷ 18,500 = 2.4%
Land: 375,900 ÷ 55 = 6830 X 55 ÷ 375,900 = 0.015%
Money: $15.2 T ÷ $8.5 T = 1.8 X $8.5 T ÷ $15.2 T = 55.9%
Which begs the question: if nuclear beats WWS so dramatically on material usage (only 2.7% and 17.2%), why does it beat WWS less impressively on money cost? (55.9% of WWS cost)
Could it be that China and South Korea have it right? That when you get right down to building them, instead of paying financing charges and legal fees, they’re actually quite affordable, at $2.7 billion (China), or $4.5 billion (South Korea)? If those Asians know something that we don't know, their nuclear advantage is 41% of WWS cost, in Korea. [$4.5 B ÷ $6.2 B X our 56% = 41%]
Only time will tell.
To visualize the advantages of the Gen 3+ nuclear course of action versus the 100% WWS Plan, Figure D presents bar graphs comparing material consumed, land occupied, and money expenditure. Both American and Korean prices are shown.
Estimated pattern of natural gas usage for purposes other than
electricity generation, during the 35-year Plan build-out.
It can be graphically integrated to find non-electric
cumulative gas consumption through 2050.
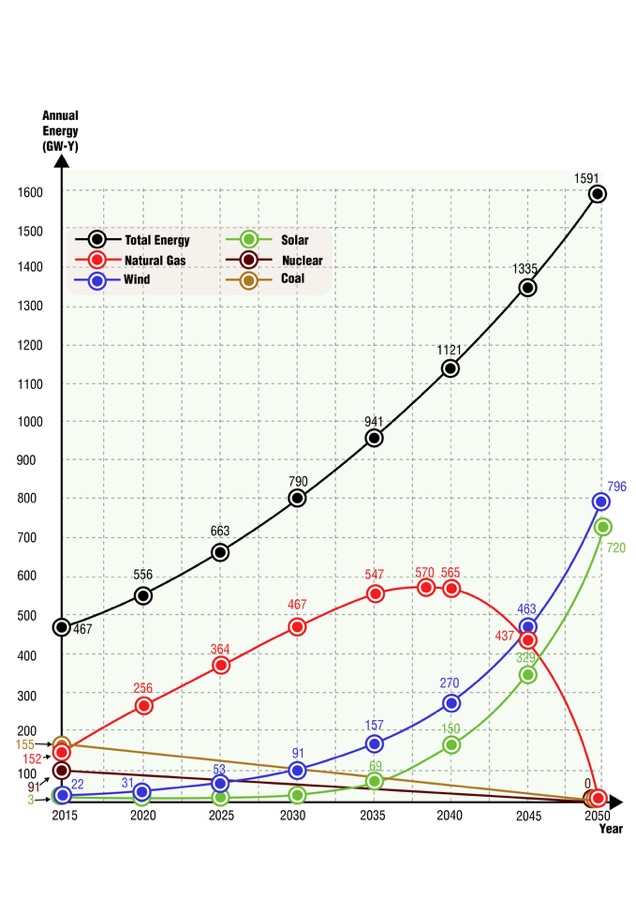
Figure D
Bar graphs of data from the tables above.
The solar and onshore wind land areas are from footnoted NREL published studies.
The red and blue area bars do not represent land reductions that may be realized in future by NREL packing-factor approach to PV solar, or aggressive concentration of wind
in the great plains at the avoidance of hilly terrain elsewhere.
The yellow land area bar represents the entire secured site area,
not the reactor equipment proper.
The yellow money bars are calculated for a fleet of 1376 reactors rated 1120 MWp.
Based on per-reactor price of $6.2 B (US) and $4.5 B (KEPCO).
Another Opinion on Dollar Cost
Besides CSP, the Plan’s Table S14 also provides an alternative source of cost figures to the NREL-sourced PV solar costs that we used earlier. And also alternatives to US DOE’s onshore wind costs, and to IRENA-sourced offshore wind.
Those numbers show rather a wide spread among scholarly studies, for every technology. One can only average them to get a representative sense. Doing so using both near-term and future (post 2014) figures for PV 48 provides the following other-opinion values, in units of $ /kWp: 49
Utility-scale fixed PV: $2077 /kWp-ac
Utility-scale tracking PV: $2683 /kWp-ac
Utility-scale PV average: $2380 /kWp-ac = $2.38 /Wp-ac
Residential rooftop PV: $3955 /kWp-dc = $3.96 /Wp-dc
Commercial rooftop PV: $3016 /kWp-dc = $3.02 /Wp-dc
Using these working figures obtained from the 100% WWS Plan’s 2014 references, the other-opinion lifetime build-out costs become much greater than the PV solar costs obtained earlier from NREL’s model projections. The costs are:
Utility-scale PV: $2.38 /W X 2,326,000 MW = $5.5 trillion for initial installation. Multiplying by our earlier-developed lifetime maintenance factor 1.8 gives
$9.9 trillion. utility PV - other opinion
Residential PV: $3.96 /W-dc X 379,500 MW = $1.5 trillion initial. Multiplying by lifetime maintenance factor 1.76 gives $2.6 trillion. residential PV - other opinion
Commercial PV: $3.02 /W-dc X 276,500 MW = $0.8 trillion initial. Multiplying by lifetime maintenance factor 1.92 gives $1.5 trillion. commercial PV - other opinion
Total PV solar: $9.9 T + $2.6 T + $1.5 T = $14.0 trillion total PV solar - other opinion
This is completely at odds with the $7.7 trillion build-out cost obtained from NREL’s modeled price declines of PV solar. We mention this other opinion for form’s sake.
Revisiting the Plan’s reference Table S14 for wind,50 but using only the lower future-build figures because we had already discounted by 20% our future estimated wind prices, gives other-opinion costs:
Onshore wind: $1822 /kWp = $1.82 /Wp
Offshore wind: $3773 /kWp = $3.77 /Wp
Here too the other-opinion lifetime costs are considerably higher than our DOE- and IRENA-derived figures stated earlier.
Onshore: $1.82 /W X 1,701,000 MW = $ 3.1 trillion initial installation. Adding our 20% lifetime maintenance expense gives $3.7 trillion.
Offshore: $3.77 /W X 780,900 MW = $ 2.9 trillion initial. Adding 30% lifetime maintenance gives $3.8 trillion.
Total wind: $3.7 T + $3.8 T = $7.5 trillion total wind - other opinion
This in contrast to $5.3 trillion obtained from IRENA’s anticipated 20% reduction relative to wind-turbine construction costs in 2014.
Total W&S build-out cost using the other opinion:
By this alternative accounting, obtained from the 100% WWS Plan’s 2014 references for PV solar, onshore and offshore wind, and CSP solar, overall lifetime cost would be $21.5 trillion overall wind & solar - other opinion
Whichever figure we take, the Plan’s lifetime cost is in the range of
15 to 21 trillion dollars. Which is about equal to our Gross Domestic
Product - or greater than.
Keep always in mind, this is with zero overbuild planned into the system, so cannot be considered the final word.
For discussion of the potential for copper and silver to act as limiting factors in the WWS construction plan, jump forward to the end of this webpage. Search for “Material Limits”.
The Wind and Solar Build-out Schedule: How Quickly?
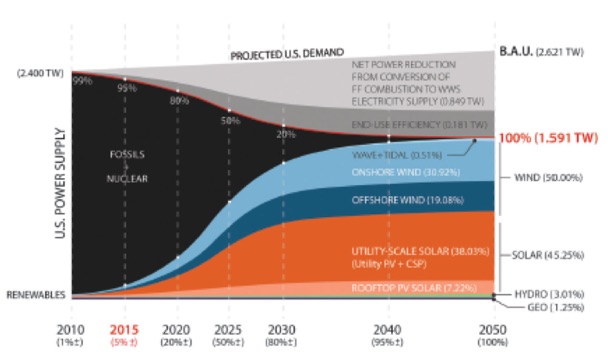
The Plan's authors put forward an S-shaped building-schedule curve in Figure 5 on page 21. Its steepest slope, corresponding to the maximum construction rate, is for the period 2020 to 2025. The build rate slackens from 2025 to 2030, slows drastically from 2030 to 2040, then tapers to a crawl for the final 10 years.
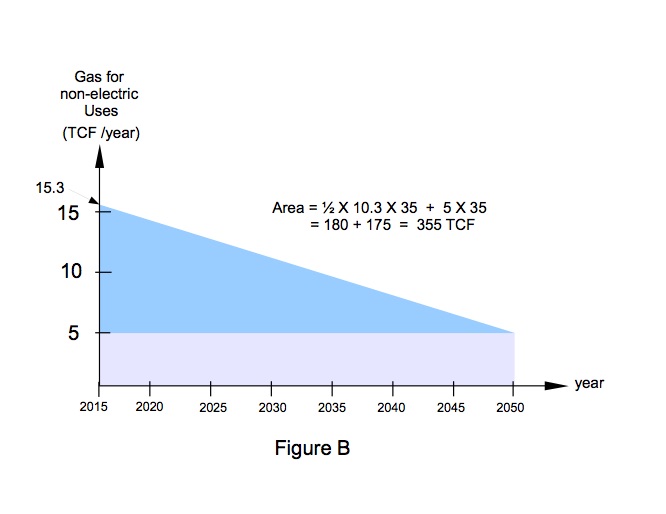
Graphically integrating that decline graph yields 175 + 180 = 355 TCF.
The 175 value comes from the bottom rectangular portion of the trapezoid; the 180 value comes from the top triangular portion.
Adding 879 TCF (for electricity) to 355 TCF (non-electricity) gives a total consumption of 1234 TCF of natural gas burned by year 2050. Using the 2000-2500 range of recoverable reserves from above, the Plan is proposing to consume between 49% and 62% of our forever endowment. [1234 ÷ 2500 = 49%; 1234 ÷ 2000 = 62%]
Going forward from year 2050 we would retain 766 to 1266 Trillion Cubic Feet of gas as our future endowment for non-combustion feedstock applications. With no growth in the above-suggested 5 TCF /yr consumption, that would last us for about 150 – 250 years.
As promised at the beginning of the article, a detailed analysis of material use and emissions, land, and costs for the Plan’s implementation is now presented.
Land, Materials, and Money Cost
for the Wind and Solar Build-Outs
The 100% WWS Plan represents the largest construction effort in human history, by far. We will now analyze each of its six main energy constituents /technologies in order to quantify the land used, the steel and concrete used, and the dollar cost for each one of the six. These energy-source constituents are: 1) utility-scale solar photovoltaic - PV; 2) residential roof PV; 3) commer-cial /governmental roof PV; 4) onshore wind; 5) offshore wind; 6) utility-scale concentrated thermal solar- CSP - with molten-salt energy storage.
All numeric values in this analysis pertain to total equipment that is to be functioning in year 2050 per Table 2, including amounts that are already in place in 2015. No distinction is made between new and already installed equipment, as is done in Table 2. That distinction is hardly worth making anyway, because such a tiny amount is already installed, except in the case of onshore wind. In 2015 the US had 74.5 GW21 of wind capacity, about 4.4% of the 1701 GW onshore-wind goal shown in row 1. (The table’s value 3.59% applied to year 2013.)
1) Utility-scale solar PV
Land Use Utility PV Solar
The National Renewable Energy Laboratory - NREL - has introduced a metric named "Capacity-weighted average land use, Direct Area". Its value for fixed-mount PV solar construction is 5.8 acres per megawatt peak-ac. For single-axis and 2-axis tracking-mount construction the land values are greater, of course. In 2012 the capacity-weighted average for all three installation types was 7.2 acres /MWp-ac.22
The conversion factor from acres to square kilometers is 1 acre = 0.004 05 km2. So 7.2 acres /MW becomes 0.029 km2 /MWp-ac for our land-density working number. [7.2 X 0.004 05 = 0.029 km2]
{In the NREL study, Table ES-1’s Direct Area value of 7.2 acres /MW is expressed in units of ac watts injected onto the electric grid. That is, it refers to the ac output power obtained from dc-to-ac electronic inverter devices and supporting equipment that have already converted the dc power produced by the solar panels themselves.
The conversion of solar-panel dc-power into electric grid ac-power inevitably entails some power loss; no conversion process performed by electrical /electronic circuitry can be 100% efficient. The actual conversion efficiency depends to some extent on ambient conditions, mostly temperature; higher ambient air temperature results in lower conversion efficiency.
As a general rule-of-thumb we assume 85% (0.85) as the nameplate dc-to-actual ac conversion ratio in situations where power data values are presented in units of dc watts. This is not the case for row 9 of Table 2 in the 100% WWS Plan, since large utility-scale solar facilities almost always have their nameplate outputs expressed in ac watts.
But this will become a relevant issue for rooftop PV installations later, where nameplate outputs are expressed in units of dc watts. That is, rooftop nameplate capacity specifications represent the output power of newly installed solar panels under ideal conditions, before conversion to high-voltage ac to be compatible with the electric grid. So it will be necessary for us to use the 85% conversion rule-of-thumb for the data in rows 7 and 8 of Table 2, which pertain to residential and commercial rooftop solar installations.}
Table 2 of the 100% WWS Plan calls for construction of solar PV utility farms with 2,326,000 MWp-ac capacity. Multiplying that number by 0.029 km2 /MW indicates a required land area of 67,500 km2 (26,100 sq mi - almost all of South Carolina).
This area is to be expressed as a percentage of US land area in Table 2, for the purpose of geographic scaling perception. The question arises whether Alaska should be counted for this purpose, since it has little solar resource, and any energy (of any kind) that it could produce would need to be transmitted over 1000 miles through Canada, out of our jurisdiction, to reach Seattle. Nevertheless the Plan does count Alaska.
Since this issue arises, let us express land percentages both ways, by counting Alaska and by not counting it.
The Plan uses area value 9,162,000 km2 for the entire US. The area of the lower 48 states is 8,134,000 km2. Therefore the percent of US land area needed for utility solar PV is:
1) 67,500 km2 ÷ 9,162,000 km2 = 0.74%, counting Alaska;
2) 67,500 km2 ÷ 8,134,000 km2 = 0.83%, for lower 48 states.
Here the 100% WWS Plan is in error. Table 2 gives just 0.189% for utility-scale PV solar.(objection)
{It must be acknowledged that land-density information for utility solar farms is confoundingly inconsistent. For instance, potential future land density can be estimated using 2016's state-of-the-art PV panel-surface electrical power density, combined with new solar farms' packing factor values. The term packing factor - PF - has been coined by NREL to mean the area of the panels themselves, expressed as a percentage of the overall occupied ground that includes spacing between the rows.
The practical choice of spacing between rows is determined by our desire to minimize the hours when a row of tilted panels blocks sunlight to its adjacent row. That problem occurs in the early morning and late afternoon, and worsens around winter solstice.
The operative numeric values for this PF approach to solar land area are:
1) About 160 W peak-ac per square meter of panel surface area (mono-silicon technology).22.3 This value is applicable to new panels working under actual field conditions of high air temperatures and moderate dust accumulation. The acronym for such real-life conditions is PTC, which can be taken to stand for Practical Test Conditions. It is distinguished from STC, referring to Standard Test Conditions, meaning ideal laboratory conditions.22.5
2) Packing factor in the US solar utility industry is settling at about 40%.22.7 On a 100,000-m2 farm, the panels themselves will have area of 40,000 m2. 22.8
When the numeric values 160 W /m2 and 40% PF are employed to anticipate future land usage, the result calculates to only 55% of the actually existing land usage in 2012 as reported by the NREL study. That is, NREL’s 0.029 value becomes 0.016 km2 /MW for future construction. (0.55 X 0.029 = 0.016)
If that 55% density can really be obtained, then the Plan’s utility solar buildout would occupy only 37,100 km² (55% of 67,500 km² from above). If that future projection proves true, the percentages of US land occupied by utility solar become:
1) 0.40% counting Alaska;
2)0.46% for lower 48 states
So instead of covering most of South Carolina it would cover only Massachusetts plus Connecticut plus Rhode Island.}
Material Use and Emissions from Manufacturing Utility PV Solar
Fixed-mount PV construction uses about 73 tonnes of steel per megawatt peak-ac, and tracking construction uses about 88 tonnes /MWp-ac.23 We average these as 80 tonnes steel /MWp-ac. The 2050 build-out of 2,326,000 MWp would therefore need 186 million tonnes of steel. [80 t X 2,326,000 MW = 186 million t] (The proper notation for “million tonnes” is written as Mt - megatonnes. We will sometimes use it.)
Today's fossil-fueled technology for steel production would necessarily remain in use during part of the 35-year period, though decreasing as we approached completion. That technology has a CO2-intensity of 1.8 tonnes CO2 / tonne steel, so would emit 335 million tonnes CO2. [1.8 t CO2 X 186e6 t steel = 335e6 t CO2]
It is anticipated that industrial process heat would be the last sector of PRI NRG to convert away from fossil energy, following electricity, transportation, and space heating. This is likely because of the capital intensity of industrial processes relative to the other three sectors, combined with the need to rely on our already existing steel- and concrete-making facilities to achieve best progress on those other sectors.
So it seems reasonable to estimate that today's CO2-intensities for steel and concrete would be applicable through perhaps three-fourths of the Plan’s build-out. For PV solar therefore, we calculate 0.75 X 335 million t CO2 = about 250 million tonnes CO2 emitted in making mounting racks to hold solar panels.
Not that we ought to be so concerned about CO2 itself when one considers that the CO2-equivalent fluoride gases NF3 and SF6, with Global Warming Potentials - GWP - of 17,000 and 24,000 per IPCC, are by-products from manufacturing PV panels themselves. This affliction is consolidated into an industry rule-of-thumb that PV panels create a global warming burden of
2 kilograms CO2-equivalent per peak watt dc, or about 2.4 kg /Wp-ac.
At utility scale that's 2400 tonnes CO2-eq /MWp-ac. So a single one of the proposed 50-megawatt PV plants in Table 2 would emit 2400 t X 50 MW = 120,000 tonnes CO2-equivalent directly from the panel-making factory, before the first load of mounting-rack steel even appeared on the job site. 46,480 such farms are called for in row 9, so their panels will themselves emit
5.6 billion tonnes of CO2-equivalent gases, swamping the 250 million tonnes caused by steel. [120,000 t /farm X 46,480 farms = 5.6 B t] (The notation “B t” for “billion tonnes” is more properly written as Gt - gigatonnes. We will adopt it.)
This would be over a 35-year period of course, so it’s a rather small portion, only 2.3%, of what the US will emit during that period under Business As Usual - BAU - fossil-burning conditions. In 2015 our BAU society emitted about
6.9 billion tonnes CO2,35 so say 241 gigatonnes CO2 emitted by year 2050. [6.9 Gt X 35 years = 241 Gt; 5.6 Gt ÷ 241 Gt = 2.3%]
5.6 billion tonnes of emissions is for utility-scale farms only, not counting rooftop PV panels. This wouldn't be so bad if solar panels would last for
60–80 years, like an advanced pressurized water nuclear reactor - APWR. But PV panels must be replaced every 25–40 years or so,23.2 more's the pity. Let us suppose that all manufacturers will eventually achieve the 40-year lifespan that the premier company, SunPower, now claims.23.4 Thus a solar farm will use up two sets of PV panels during the lifetime of one nuke. So bump that 5.6 number up by 2 X, to 11.2 billion tonnes CO2-eq emitted per lifetime. Now the emissions don’t seem quite so small, at almost 5% of BAU. [11.2 Gt ÷ 241 Gt = 4.6%]
Summarizing material use and emissions for the Plan’s utility PV solar, we have:
Steel: 186 million tonnes, which would be about 6% of our 35-year total steel production (81 Mt /yr) under BAU. That’s manageable.
CO2 from steel: 250 million tonnes.
Greenhouse gases over an entire lifetime: 11.2 billion tonnes CO2-eq, which swamps steel’s emissions of 250 Mt. Combined, they give an atmospheric burden of 11,400 Mt CO2-eq.
Note that 11.2 billion tonnes CO2-eq derives from panel manufacture only. It doesn't account for GHG emissions from recycling old panels.
The 2.0 kg CO2-eq /Wp-dc rule-of-thumb could perhaps be improved by better gas-capturing techniques in the manufacturing process, which might be introduced during the build-out period. If improvements are possible, they would surely entail higher panel cost. If they’re not possible, we’re stuck with a big GHG load.
Money cost Utility PV Solar
NREL projects that utility-scale fixed-mount PV projects begun in 2016 will have total system cost = $1.71 /Wp-ac,24 not counting land expense. For tracking-mount the figure is $1.79 /Wp-ac.25
Ac cost figures are determined in part by the conversion efficiency of the electrical equipment that converts panel-nameplate dc voltage into grid-compatible ac. The above dollar figures assume conversion efficiency of 83%, which NREL has adopted for ground-placed solar equipment. That is slightly lower than the industry rule of thumb for inverter efficiency, namely 85%. Presumably this choice accounts for recent experience at existing solar farms, perhaps related to dust build-up on the panels’ surfaces. NREL continues to use 85% for rooftop installations.
We will average the fixed- and tracking-mount costs for a working figure of $1.75 /Wp-ac for 2016 construction. Let us first price the Plan’s utility solar buildout using 2016 dollar cost structure. After establishing the current price we will attempt predictions of future cost reductions over the 35-year building period.
Table 2’s row 9 goal of 2,326,000 MWp-ac, at $1.75 /MWp-ac, calculates to a national cost of 4.1 trillion dollars. That’s not counting land purchase or lease, and also not counting electric transmission infrastructure to connect isolated tracts to an existing high-voltage line. Which transmission infrastructure runs in the one to two million dollars per mile cost range. The $4.1 trillion is just to get the farms themselves functional, in a not-too-hot and dusty environment.
Future design and manufacturing improvements are expected to lengthen PV panel life to 40 years, for 2 sets of solar panels during a 60–80 year life cycle, as mentioned above.
The electronic inverters also must be replaced several times. How often depends on their cycling conditions - the number of heat-up /cool-down cycles that they endure. It appears that these circuits have a life expectancy of approximately 10,000 cycles. Therefore if they cycle an average 3 times per day due to cloud intermittency, they need to be replaced every 9 years or so. [3 cycles /day X 365 days /yr X 9 years = 9855 cycles] If they’re located where conditions are always sunny they may last for about 27 years.
Let us estimate US average operating duration in the teens for dc inverters, therefore requiring three or four replacements over a life cycle.
PV panels themselves represent about 44% of the total system’s price, with the dc inverters accounting for 7%, and installation labor about 9%.26 So a complete equipment change, say at 40 years after initial construction, adds 60% to the farm’s lifetime cost. [44 + 7 + 9 = 60%]
Two additional inverter replacements will add another 20%. [(7% + 3% share of labor) X 2 = 20%] Thus a farm’s lifetime cost can be estimated as 180% of it's initial cost, a factor of 1.8. That would drive our national utility-scale PV fleet up to 1.8 X 4.1 trillion = about $7.4 trillion lifetime cost.
The fuel is free, so $7.4 T is supposed to pay for 31% of US Primary Energy for at least 60 years, per row 9.
2) Residential rooftop PV solar
The 100% WWS Plan in row 7 calls for new solar panel installations on over 75 million residential houses with an average capacity of 5 kW peak. Combined with the approximately 700,000 houses that already have rooftop panels, this build-out is intended to provide 3.98% of our national PRI NRG in 2050, or 63 GW-y /year. [Table 2, row 7, "all-purpose load" column; 3.98% X 1591 = 63 GW-y]
But the Overview section maintains that there would occur a 17.8 GW-y shortfall because 2015’s actual residential CF of 14.4% differs so sharply from the Plan’s implied CF of 19.5%.27 Refer to footnote 27 for distinctions drawn between utility-scale, commercial flat-roof, and residential sloped-roof solar capacity factors.
The nice thing about roofs is that no land is required. So we proceed directly to material usage and CO2 emission.
Material use Residential PV Solar
Residential solar roof-racks are aluminum, which is an industry with a rule-of-thumb stating 17 kg aluminum per kilowatt peak dc. The Plan’s row 7 value 379,500 MWp is assumed to refer to the actual panel output stated in dc units, as explained in footnote No. 27. Therefore total aluminum needed for new and existing residential solar is calculated as 17 kg Al /kWp-dc X 379,500 MWp-dc = 6.45e9 kg aluminum, or about 6.5 million tonnes of aluminum.
CO2-intensity for fossil-fueled aluminum manufacture is slightly worse than for steel, at 2.0 tonnes CO2 /tonne Al. This would imply 2.0 t CO2 X 6.5 M tonnes Al = 13 million tonnes CO2 from aluminum. We could apply the same three-fourths estimate that we proposed for steel over the 35-year duration, but why bother? That 13 M t amount is trivial compared to the 250 million tons CO2 from steel. Besides, PV-panel exotic GHG emissions would swamp the emissions from metal mounting-supports anyway under current manufacturing methods.
Recalling the industry-standard 2.0 kg CO2eq /Wp-dc due to NF3 and SF6, row 7 gives 2.0 kg /W X 379,500 MW = 759 million tonnes CO2eq from residential rooftop panels. Remember that solar panels must be replaced at least once during a 60-year lifespan, so multiply any panel-emissions amount by 2. That gives 759 Mt X 2 = 1.5 billion tonnes CO2eq in a lifespan for residential PV. Aluminum's 6.5 Mt CO2 is negligible, as anticipated.
As was done earlier for utility-scale PV farms, it is again helpful for appreciation of scale to compare to our fossil-fueled BAU emissions of
6.9 Gt CO2 /yr. For US residential solar the 60-year lifetime emission would be only one-fifth of BAU's emissions for just one single year. [1.5 Gt residential PV ÷ 6.9 Gt BAU = about 1 /5] As bad as exotic GHGs are, they pale to insignificance in comparison to fossil-fuel combustion.
Money Cost Residential PV Solar
NREL publishes a total system cost = $2.93 /Wp-dc28 for sloped-roof residen-tial solar installations in 2016. Of that, $1.10 goes for panel, inverter, and labor, or 38% of total cost.29 The Plan's 379,500 MW X $2.93 /W gives about 1.1 trillion dollars for initial installation.
We can anticipate one simultaneous replacement of panels and inverters at age 40 costing 38% of the initial amount, plus three additional replacements of inverters due to more frequent on-off cycling for town rooftop placement compared to open field operation. So the lifetime replacement expense would be about 38% + 33%29.1 = 71% of initial amount. Thus lifetime cost rises by a factor of 1.71 to $1.9 trillion.
That’s not counting recycling of old panels, which is a mechanical /thermal /chemical process with its own non-negligible cost and carbon footprint. After the old panels have been shredded and milled into fine particles, the vinyl-like foil material is separated from the glass and aluminum bulk by a high-temperature thermal process. Then, from silicon-based cells, the copper, silver and lead metal content must be removed by an acid-leaching chemical process. Non-silicon thin-film PV cells contain exotic and /or toxic metals (cadmium, especially) that likewise must be removed chemically.
3) Commercial /Governmental rooftop PV solar
Energy production implied by row 8 of Table 2 for commercial rooftop solar is dubious, as the 19.5 GW-y commercial PV shortfall derived in the Overview section suggests. Refer to footnote 27 for details.
Material Use Commercial PV Solar
For flat-roof installations the solar industry estimates 159 kg30 of steel racking per dc kilowatt of capacity, or 159 tonnes /MWdc on large scale. The 100% WWS Plan's Table 2, row 8 calls for 276,500 MWdc, with less than 1% already functioning, like residential. It would require 159 t /MW X 276,500 MW =
44 million tonnes of steel.
We will pass over the CO2-footprint of that steel, knowing it's negligible in com-parison to the fluoride greenhouse gases emitted by PV panel manufacture.
At the PV-standard 2.0 kg CO2-equivalent /Wp-dc, we have 2.0 kg X 276,500e6 W = 553 million tonnes CO2eq. Replacing the panels every
40 years increases that by a factor of 2 over a lifetime, so 2 X 553 M =
1.1 billion tonnes CO2eq per lifetime under our current manufacturing /gas-capture regime. It’s in the same range as the 1.5 billion tonnes emitted by residential PV panels, and bearing a similar relation (one-sixth, now) to our annual BAU carbon-fuel emissions.
Panel recycling is not counted, as usual.
Money Cost Commercial PV Solar
NREL publishes 2016 flat-roof total system cost to be $2.13 /Wp-dc.31 Of that, $0.97 goes for panels, inverters, and labor - about 46%.32 For Table 2's row 8 build-out, we calculate 276,500e6 W X $2.13 = $600 billion for initial installation. Replacing all equipment once and dc inverters three times additionally will boost the lifetime cost by 46% + 33%32.1 = 79%. For a total cost of 1.79 X $600 billion = 1.1 trillion dollars. Plus recycling.
Total Cost - All three PV solar categories combined
Combining all three PV solar placements using 2016 prices, we're looking at $7.4 T + $1.9 T + $1.1 T = 10.4 trillion dollars. That's to provide 38% of our society’s PRI NRG for a lifetime (rows 7, 8 and 9, "all-purpose load" column).
As mentioned earlier, utility-scale PV solar expects total system costs to continue their decline. The downward trends for all three PV placements were analyzed by NREL in their Photovoltaic System Pricing Trends report in 2015.32.5 That study presents past-modeled prices since 2010, also actual system prices since 2007, and also model-projected prices for years 2017 and 2018.
Past-modeled predictions for 2010 and 2011 matched very well the actual system installed costs in those two years. But in-advance modeling predictions for 2012 through 2015 were too optimistic. Actual installed costs did indeed decline sharply in those years, from $3.80 /Wdc in 2011 to
$1.80 /Wdc in 2015, but the models had predicted even steeper declines. So utility PV analysis models have a track record of over-expectations regarding cost reduction.
Going forward now from 2016, assuming incremental year-over-year improvements in PV cells’ solar-to-electric conversion efficiency, current models project a $0.20 /W reduction in 2017 and a further 10-cent reduction in 2018.32.5 If they’ve got it right this time, total system cost for fixed-tilt in 2018 will be 30 cents lower than 2016’s $1.42 /Wdc, namely $1.12 /Wdc. That would give nameplate ac cost of $1.12 /Wdc ÷ 0.83 = $1.35 /Wac, which is 21% lower than 2016’s $1.71 /Wac.
The graph has no expectation stated for 2019 but the shape of the curve since 2010 clearly shows leveling off. So after 2018 the models indicate no further cost reductions realizable from labor productivity or from balance-of-system - BOS - the expression that encompasses all material other than the PV modules.
Regarding those PV modules themselves, the NREL study US Solar PV System Cost Benchmarks, published in 2016, anticipates the effects on total system cost of greatly improved solar-to-electric conversion efficiency.32.7 This matter has to do with basic physics research, not improved manufacturing and installation practices. The study examines the consequences of field-operation efficiencies all the way up to 60%. Photovoltaic cell makers do not expect their product to approach 60% in the foreseeable future, but some do entertain an ambitious goal of 25% solar-to-electric conversion outdoors. Others think that target would require a major research breakthrough, and so is unlikely.
The Cost Benchmarks study asserts that utility PV system cost would decline by an additional 7% if the 25% conversion goal could be attained.32.7
In summary, it seems that we are on the cusp of a final 21% cost improvement from BOS, with a possible additional 7% reduction coming gradually over the years. Let us accept these benefits and assign 28% as the mid- to long-term cost reduction for the Plan’s utility PV solar over a 35-year period. In that case the Plan’s utility-scale PV solar cost will shrink to $5.3 trillion.
[28% X $7.4 T = $2.1 T; $7.4 T – $2.1 T = $5.3 T]
Residential and commercial rooftop PV prices also are declining, as illustrated in the 2015 NREL study. Past-modeled system prices from 2012–2015 again were over-optimistic, more so than for utility PV. Going forward from 2016 with residential and commercial combined as "distributed" PV (the graph’s gray boxes), analytic models project a $0.30 /W reduction in 2017 and a further
16-cent reduction in 2018.32.5 So distributed residential and commercial PV is set to decline by 46 cents from 2016’s combined $3.10 /Wdc.
This represents a 15% price decline. The graph is not clear about leveling off in 2018. For residential and commercial PV pricing in the Plan buildout, let us expect a near-term 15% cost reduction due to BOS, labor, and year-over-year incremental efficiency gain.
For the longer term, careful inspection of the solar-to-electric efficiency graph in the Cost Benchmarks 2016 study shows that if cell-makers ever reached their 25% goal, commercial PV would enjoy an additional 7% system reduction, like utility PV. Residential would benefit slightly more, by 9%. We will use the average 8%.
Adding together the near-term and long-term percentages as was done for utility PV, we will claim 15% + 8% = 23% cost reduction for residential and commercial PV. Under that assumption, the Plan’s 35-year costs become:
Residential PV: $1.9 T - $0.4 T = $1.5 T
Commercial PV: $1.1 T - $0.2 T = $0.9 T
All three solar placements combined come to $5.3 T + $1.5 T + $0.9 T = $7.7 trillion. all PV solar
In fairness to human ingenuity we will discard PV 2016 prices and adopt this lower dollar amount for the Plan’s PV buildout.
Keep in mind, this is with zero overbuild proposed in the system, so is not realistic in terms of achieving a reliable all-electrified society.
4) Onshore wind
Land Use Onshore Wind
National Renewable Energy Laboratory in 2009 surveyed 172 American utility-scale wind farms to determine land area usage. Their average land-density was 0.345 km2 /MWp.33
Those 172 wind farms were in operation, or under construction, or waiting the start of construction, as of March 2009. NREL pointed out that some were on hilly /uneven terrain and others were on open flat terrain, resulting in large deviations in land use density.
Setting aside 14 outliers, the other 158 wind projects ranged from 0.14 km² to 1.0 km² per megawatt of capacity, a factor-of-7 difference. Though NREL didn't explicitly say it, surely the low end of the range refers to large-capacity wind farms on open flat terrain with the high-end of the range referring to hilly projects with the turbines concentrated on hilltops or ridge lines, which also encompasses hillsides and valleys where turbines are sparse.
To the extent that the 100% WWS Plan is able to site future onshore wind capacity in our flat central plains, the national average land density will be closer to 0.14 km² /MW. To the extent that the Plan finds itself required to use shore lines and the high ground in hilly regions, the national average land density will approach closer to 0.345 km² /MW.
The specific turbines that the plan proposes to use are the REpower Co (now renamed Senvion Co) 5-MW units with blade-swept diameter = 126 meters. They sit atop 100 m-tall towers – the height of a 30-story building. Because of their enormous blade length and height, it may be possible to achieve lower land densities (reduced land usage) than were possible in 2009.
The Plan's lead author Mark Jacobson has communicated to this author that The Solutions Project expectation is 0.089 km² /MW for new wind projects on open flat terrain. If that density value can be shown feasible then the overall national average for onshore wind will be some value between 0.089 km² and 0.345 km² /MW, depending on the relative concentration in our great plains states.
The Solutions Project 50-states infographics,12.8 seems to suggest about two-thirds as the great plains concentration. Adopting that ratio - 0.67 - as our working assumption, we can calculate the weighted average of the minimum and maximum values. Weighted average = 0.67 X 0.089 km² + 0.33 X 0.345 km² = 0.173 km² /MW. Let us round to 0.17 km² /MW as our working figure for onshore wind discussion.
The 100% WWS Plan in row 1 of Table 2 calls for 1,701,000 MWp of onshore wind generating capacity . 74,500 MW has already been installed at the end of 2015. Total land area for existing plus new farms would be 1,701,000 MW X 0.17 km2 /MW = 289,200 km2 (111,700 sq mi).
As we did for utility-scale PV farms, so for wind we calculate US land-area percentages two ways; including Alaska, or counting only the lower 48 states.
1) With Alaska: 289,200 km2 ÷ 9,162,000 km2 = 3.2%
2) Lower 48 states: 289,200 km2 ÷ 8,134,000 km2 = 3.6%
However, the Plan maintains that only 1.59% of US land area is required for new wind, which is nearly all of the total, 96.4%. Refer to Table 2, row 1, the far-right column headed "percent of US land area". This is quite a large discrepancy(objection).
Working backward from 1.59% to ascertain the land area expected by the Plan’s authors gives 1.59% X 9.162e6 km2 = 145,700 km2 (56,200 sq mi).
The discrepancy between our calculated 289,200 km2 and the Plan-asserted 145,700 km2 can best be appreciated by recognizing that the larger area would occupy all of Kansas, all of West Virginia, and half of Vermont. The Plan’s smaller land area would occupy only all of Illinois.
Material Use and Manufacturing Emissions Onshore Wind
There is well-established steel- and concrete-usage data for a wind turbine of size 2.5 MW, specifically the General Electric model GE 2.5xl. The usage values are:34
Steel: 289 tons /2.5-MW turbine = 115.6 t /MWp
Concrete: 1078 tonnes /2.5-MW turbine = 431 t /MWp
The 100% WWS Plan anticipates using much larger turbines of 5-MW name- plate capacity. There is no material-usage benefit expected from such a jump in size. This is because a turbine’s wind-energy capture capability is determined by the swept area of its rotor blades, which increases as the square of the swept area’s radius - blade length, essentially. Area = 3.14 X R2.
But the material-usage and manufacturing cost of a turbine blade increases more rapidly than by the square power (2 power) of its length. Per an NREL study, blades’ material-use and cost tend to increase by the cube power
(3 power) of length, or as the 2.5 power.35
Regarding the wind tower and foundation, their steel and concrete mass also increases as the 2.5 or 3 power. This is a natural consequence of the tower's cross-section area, in square meters, combining with its height, in meters, to form its volume, in cubic meters. So an entire turbine structure’s volume and mass tend to be cubic functions (3 power), rather than square functions
(2 power).
With energy capture increasing as the 2 power and volume and mass increasing as the 2.5 or 3 power, it happens that turbines exceeding about
3-MW capacity have somewhat greater per-unit consumptions of steel and concrete, not less. We will not attempt a quantified estimate of this worsening effect for the Plan’s proposed rated capacity of 5 MW . For simplicity let us assume that onshore wind farms will standardize on 2.5 to 3-MW units. So we continue with the steel and concrete usage values of the 2.5-MW model from above.
Future wind build-out would consist of 1,626,500 MWp. [1,701,000 MW goal minus 74,500 MW in 2015] It would require these quantities of steel and concrete:
115.6 t steel /MW X 1,626,500 MW = 188 million tonnes steel
431 t concrete /MW X 1,626,500 MW = 701 million tonnes concrete
CO2 emissions due to steel and concrete manufacture can be estimated as was done for PV solar, with a three-fourths rationale for the 35 years. Therefore
CO2 emissions from steel = 0.75 X 1.8 t CO2 X 188e6 t steel =
254 million tonnes CO2
CO2 emissions from concrete = 0.75 X 1.2 t CO2 X 701e6 t concrete =
631 million tonnes CO2
Total CO2 from onshore wind would be 254 + 631 = 885 million tonnes CO2, emitted over 35 years.
For scale appreciation, that's merely 13% of the 6900 M tonnes CO2 emitted annually by US fossil fuels.36
Money Cost Onshore Wind
The US Department of Energy - DOE - reported an average cost of $1.71 /Wp37 for onshore wind projects installed in 2014. Average turbine size was 1.9-MW peak capacity.38
Future construction will probably use slightly larger turbines, as stated above. A 2011 study by the International Renewable Energy Agency - IRENA - estimated that manufacturing economies and other considerations are likely to reduce overall wind costs by 12% by year 2020, and 23% by year 2040.39
Let us choose 20% from within that range to project average cost over the
35-year build-out. Therefore we have 0.80 X $1.71 = $1.37 /Wp for projected average cost. $1.37 /W X 1,626,500e6 W of new wind = 2.2 trillion dollars for initial construction.
The DOE cost report included connecting to a neighboring electric transmission line, but did not include construction of a separate line to serve a remote location. As usual, land purchase /lease costs were not included.
Just as for PV solar panels, we are gaining knowledge and experience about maintaining aging turbines. Early results seem to indicate that it is necessary to refurbish the blades themselves and the equipment inside the nacelle every 15–20 years of operation. Nacelle refers to the vessel sitting atop the tower, containing the electric generator and its mechanical driveshaft and gearing.
Typical refurbishment cost seems to be about 10% of installation cost.40 With a 20-year schedule there would be 2 such refurbishments per 60-year reactor lifetime; with a 15-year schedule, 3 refurbishments. Let us assume the 20-year schedule. Thus 2 X 10% = 20% lifetime refurbishment costs. 20% X $2.2 T initial = $0.4 T for refurbishment. That gives $2.2 T + $0.4 T = $2.6 trillion lifetime equipment cost for the Plan’s proposed new onshore wind.
Recycling cost of the composite fiber turbine blades is not included.
Summarizing onshore wind’s build-out, we have for estimates: Onshore Wind
Steel: 188 million tonnes
Concrete: 701 million tonnes
CO2 from steel and concrete: 885 million tonnes
Lifetime money cost: $2.6 Trillion Onshore wind
Land use (new + already built): 289,200 km2 (111,700 sq mi).
That is, 3.6% of the lower 48 states would be occupied by wind farms.
5) Offshore Wind
The IRENA 2011 study reported offshore wind costs to be about 2 X onshore costs.41 The study did not specifically consider steel and concrete usage, but it seems reasonable to assume a 2 X factor there also. Certainly so for seabed tower foundations - not floating.
Let us multiply all onshore values by 2 X to get working calculation values for offshore wind.
Cost: 2 X $1.37 /Wp = $2.74 /Wp
Steel: 2 X 115.6 t /MWOnshore = 231 t /MWOffshore
Concrete: 2 X 431 t /MWOnshore = 862 t /MWOffshore
Money Cost Offshore Wind
The Plan envisions 780,900 MWp of offshore wind capacity in row 2 of
Table 2. So initial installation would cost $2.74 /Wp X 780,900 MWp =
2.1 trillion dollars.
Assuming a 15-year schedule in the harsher environment, there would be
3 refurbishments per 60-year lifetime. If 10% of initial cost proves correct for offshore refurbishment also, we can calculate 3 X 10% = 30% lifetime refurbishment costs. 30% X $2.1 T = $0.6 trillion for refurbishment.
For lifetime total cost of the Plan’s offshore build-out we have $2.1 T + $0.6 T = $2.7 trillion.
Material Use And Emissions Offshore Wind
Multiplying the Plan’s 780,900 MW by offshore's 2 X greater per-unit values of steel and concrete yields
Steel: 780,900 MW X 231 t /MWOffshore = 180 million tonnes steel
CO2 from steel = 180 M t X 1.8 t CO2 = 325 million tonnes CO2 Offshore
Concrete: 780,900 MW X 862 t /MWOffshore = 673 million tonnes concrete CO2 from concrete = 673 M t X 1.2 t CO2 = 808 million tonnes CO2 Offshore
Total CO2 emissions over 35 years = 325 + 808 = 1133 million tonnes CO2
Summarizing offshore wind’s proposed build-out, we have for estimates: Offshore Wind
Steel: 180 million tonnes
Concrete: 673 million tonnes
CO2 from steel and concrete: 1133 million tonnes
Lifetime Money Cost: $2.7 Trillion
Area Offshore Wind
No dry land is occupied, but seascape is profoundly altered. Nine recent offshore installations, including the London Array, the world's largest, average 0.23 km2 /MWp.42 Assuming that The Solutions Project’s expectation of
0.089 km2 /MW proves realizable on open flat land using late-model gargantuan turbines, it will be realizable offshore too. At that density the Plan’s offshore farms would occupy 0.089 km2 /MW X 780,900 MW =
69,500 km2 (26,800 sq mi). That's half the area of Florida.
To summarize the Plan’s combined onshore and offshore wind requirements for land and money: On land we would occupy area equal to Kansas, West Virginia and half of Vermont. In the ocean we would occupy an area from Disney World to Miami. The 60-year cost would be $2.6 T + $2.7 T =
$5.3 trillion. Combined Onshore & Offshore Wind
That's expected to provide 50% of our nation’s PRI NRG for a lifetime (rows 1 and 2, the column "all-purpose load").
Keep always in mind, our descriptions refer to a system that contains no overbuild.
6) Concentrated Thermal Solar - CSP
The Plan’s CSP specifications appear in rows 10 and 11. Combined, they have peak capacity of 363,700 MW, or 363.7 GW. Their percentages add to 11.68% of our 2050 end-use load value 1591 GW-y; so CSP expects to produce 185.8 GW average power. [0.1168 X 1591 = 185.8] The technology’s implied capacity factor is thus 185.8 GWavg ÷ 363.7 GWp = 51.1%.
Such a CF value is everywhere impossible if CF is defined in the classic manner. (objection) That is, actually produced annual energy as a percent of potential annual energy if the source could operate at its peak capacity for all 8760 hours of the year.
However, capacity factor values for CSP plants with molten-salt thermal energy storage are misleadingly defined and presented, for publicity purposes. They are artificially boosted by an accounting gimmick that understates the true solar insolation power capacity of the reflectors in the solar field. That understatement is adjusted to match the maximum power output from the farm’s turbine /generator equipment, which has been deliberately undersized.
The solar farm’s steam-turbine equipment boils water by passing it through a hot-fluid (molten salt) heat-exchanger. But the heat-exchange equipment and generator are sized so they cannot handle all the thermal energy that the reflecting mirrors are capable of concentrating into the molten-salt fluid. Therefore the excess heat energy must be routed into a temporary storage tank containing 400-degree molten-salt fluid that does not participate in daytime power production. That energy is held in the large tank till after sunset, then it is tapped to make fresh steam when the turbine /generator equipment is no longer receiving energy via the solar reflectors.
In this way a CSP solar farm can continue generating electricity during night hours; so it seems that it's capacity factor has been improved.
It's a good idea, societally speaking. The solar industry has chosen to use a good idea to make misleading public-relations statements about capacity factor.
To succeed at the practice of extending hours of operation, a concentrating solar site must contain:
a) many more reflecting panels than would otherwise be required to run the generator;
b) great quantities of extra molten salt, for storing the excess heat produced by those extra reflectors;
c) large holding tanks with associated plumbing, for pumping and containing the extra salt fluid; and
d) natural gas heating equipment to make sure the fluid doesn't solidify if the following day is sunless.
Constructing all this extra equipment makes CSP solar more expensive than PV solar, and involves greater material use.
CSP Land and Material Use CSP Solar
Discussion of the Plan’s “Number of new plants” column aiming for 2273 + 1364 = 3637 CSP plants, with their 100-MW nameplate rating, must be based on average power or on annual total energy production, in order to avoid possible misinterpretation of the peak nameplate rating figure. This is a consequence of the "capacity factor" issue, as explained above.
Referring to the 185.8 GWavg value developed from the 11.68 percentage of 2050's PRI NRG, we can make a useful comparison of the Plan’s proposed CSP build-out to the facility at Andasol, Spain, which is the world’s largest CSP plant with molten-salt storage.
Completed in 2011, the Andasol plant has been averaging annual energy production of 495 GW-h.43 This is more usefully expressed as average power = 56.5 MWavg. [495e9 W-h /yr ÷ 8760 h /yr = 56.5e6 Wavg]
Andasol publicizes a capacity factor of 41%, roughly similar to the Plan’s implied 51% CF. Therefore Andasol must have a roughly similar ratio of solar reflectors relative to molten-salt thermal storage equipment; roughly similar, that is, to the ratio envisaged for the Plan’s 100-MW CSP farms.
(Actually, the Plan’s somewhat higher 51% CF [compared to Andasol’s 41%] means there would be heavier weighting of thermal storage relative to solar-field panels, in the US plants. We are passing over that weighting difference for the sake of ease of calculation.)
The ratio of the Plan’s total CSP average power to Andasol’s average power is 185.8 GWavg ÷ 56.5 MWavg = 3288 X greater. Thus, for estimating land and material required in the Plan’s CSP build-out, we will simply multiply the Andasol figures by 3288.
Land CSP Solar
Andasol occupies 5.85 km2,44 so the Plans' buildout would occupy 3288 X
5.85 km2 = 19,200 km2 (7400 sq mi). This calculation agrees well with Table 2’s 18,000 km2 from rows 10 and 11 combined.
[0.123% + 0.074% = 0.197%; X 9.162e6 km2 =18,000 km2]
Material CSP Solar
Andasol used 57,300 tonnes of steel and 184,000 tonnes of concrete.45 So the Plan’s CSP build-out would use:
Steel: 3288 X 57,300 t = 188 million tonnes steel
Concrete: 3288 X 184,000 t = 605 million tonnes concrete
CO2 from steel and concrete: 1060 million tonnes CO2
[188 X 1.8 t + 605 X 1.2 t = 1060 Mt CO2]
CO2 emissions from reflector glass manufacture are negligible.
Money Cost CSP Solar
In the Plan’s Table S14 on pages 91 and 92 (frames 93 and 94) a range of costs is presented for CSP with storage. Of course an actual facility’s cost depends on how much storage it has - that is, how many hours it can continue operating after sundown. As a rule, the higher the published capacity factor, the more hours it can operate. Therefore the higher will be the per-unit money cost.
On p. 91, near-term CSP w /storage ranges from $6000 to $8500 per kilowatt peak-ac. Future costs on p. 92 are anticipated to decline to $3500–
$6000 /kWp-ac. Ignore the $8608 entry in the Lazard column; it is a mistake. Everyone expects future costs, for all technologies, to decrease with economies of scale and with manufacturing experience.
Let us average the Table’s cost ranges for near-term and for future construction to obtain a working figure. For near-term it's $7046 /kW; for future its $4839 /kW.46 Some plants would be built soon, most in the future, but we will use the simple unweighted average of $5942 /kW. Converting to per-watt basis for consistency with PV solar and wind, we have $5.94 /Wp-ac as a working figure.
Figure 5
Graph of the Plan’s proposed schedule for building wind and solar
generating capacity from 2015 – 2050, and for reducing demand.
The vertical axis variable can be regarded as annual average power,
such that US Primary Energy yearly consumption is that value,
in units of terawatt-years,TW-y.
The value 2.400 TW-y would more often be expressed as
2400 GW-y of energy, per year.
As presented, the graph misstates US Primary Energy
of the four societal sectors in year 2010 (objection).
The correct value is 3261 GW-y. (Footnote No. 51.)
Repeating carefully for the solar buildout task in Table 2, the specific values are:
d) Solar energy to be obtained in year 2050 = 720 GW-y. Add solar rows 7, 8, 9 and 10 to get 45.25% of Table 1's 1591 GW-y. Therefore 0.4525 X 1591 = 720 GW-y.
e) In 2015 actual US solar energy production was 3 GW-y.16 This is the initial value from which we would start compounding.
f) To grow at a compounded rate that boosts 3 to 720 GW-y /year would require an annual growth rate of 16.95%. Implying a factor of increase = 1.1695, exponentially compounded. 3 X (1.1695)35 = 3 X 239.9 = 720 GW-y.
The exponential growth curve for solar is the green line in the Figure A graph.
The Plan eliminates coal and nuclear fission from the mix of electric sources by 2050. Their phase-outs are represented by the two assumed-linear declines near the bottom of Figure A. The brown line shows coal, purple shows nuclear.
Dammed hydroelectric energy is scheduled to increase from its initial 28.7 GW-y17 in 2015 to 47.9 GW-y (row 5 shows 3.01% of the 1591 GW-y goal). Most of this 67% increase would have to be accomplished by holding the turbine gates open for extended hours, since the proposed new capacity is minimal, at only 4.13% (row 5 indicates 100% – 95.87% = 4.13%). That energy increase was assumed to be linear in calculating the natural gas data points of Figure A, though hydro itself is not drawn on the graph.
Likewise for geothermal and ocean-wave generation. Their construction could reasonably be assumed to occur linearly because they are so small, at only 1.76% of total capacity (rows 3, 4 and 6). They slightly affect calculated natural gas consumption but they are not graphed in Figure A. Nor are the Plan’s phase-outs of biomass (1.6%) and petroleum (0.7%).
Regarding conventional hydro, it seems dubious for the Plan to expect extended hours of turbine flow, given recent years' drought-related lower water levels in Lake Mead and Lake Powell (Hoover and Glen Canyon dams).
A profoundly important consequence of the equipment expansion /realignment proposed in Table 2 is that natural gas consumption for electricity generation would increase tremendously during the middle years of the build-out. As total renewable energy demand rises exponentially, shown by the black line, the combined productions from wind, solar, coal, nuclear and hydro (blue, green, brown and purple lines, plus hydro) would not satisfy the black line demand. The shortfall must be provided by natural gas, indicated by the red curve.
The red-curve data points have been obtained by subtracting the combined data values for wind, solar, coal and nuclear curves, also hydro, from the black total-demand curve. As shown by that red curve, natural gas electric generation (not counting residential and commercial heating and industrial processes) would rise from 152 GW-y in 2015 to a peak of 570 GW-y in years 2038 and 2039, then decline rapidly to zero during the final 11 years.
This consequence has utmost importance regarding America's gas reserves, which provide the feedstock for production of nitrogen fertilizer, plastics, synthetic fabrics, and some medicines.
Graphical integration of the area under the red curve represents the total electric energy obtained from natural gas over the 35-year duration. From that knowledge we can calculate the volume of gas that would need to be burned, and so relate it to our recoverable reserves. This will now be undertaken with the understanding, if it even needs repeating, that hydrocarbon reserves are a one-time endowment to human civilization. They accumulated on planet earth through geologic eons. When they're gone, they're gone forever from the viewpoint of human affairs.
Graphical integration is the process of counting the major squares, their area, in each of the 14 columns beneath the red curve. Each column, the width of one square, represents 2.5 years. The height of one square represents
100 GW-y /year. Therefore the area of one square represents 250 GW-y.
[2.5 years X 100 GW-y /year]
Beginning from the left, the first column (years 2015 to 2017-1/2) contains about 1.8 squares. The second column contains about 2.3 squares. The third column contains about 2.8 squares. And so on.
The 14 contributions become
1.8 + 2.3 + 2.8 + 3.4 + 3.9 + 4.4 + 4.9 + 5.3 + 5.6 + 5.7 + 5.4 + 4.7 + 3.6 + 1.6 = 55.4 squares.
With each square representing 250 GW-y, we calculate 55.4 sq X 250 GW-y /sq = 13,850 GW-y of electric energy generated by natural gas through year 2050.
The volumetric energy density of US natural gas averages 15.76 GW-y per Trillion Cubic Feet - TCF. This can be derived by dividing US annual electric production from gas by annual gas volume consumed for electricity. In 2015 those values were 152.4 GW-y 18 electricity generated from gas, and 9.67 TCF 19 of gas consumed. 152.4 GW-y ÷ 9.67 TCF = 15.76 GW-y /TCF.
Therefore the volume of natural gas that would be required to produce the 13,850 GW-y indicated by graphical integration of the red curve is given by 13,850 GW-y ÷ 15.76 GW-y /TCF = 879 TCF burned for electricity during those 35 years. To repeat, this does not include gas used for space heating and manufacturing processes, which amounted to 15.33 TCF20 in 2015.
If gas-fracking goes forward everywhere within US jurisdiction, our natural gas recoverable reserves are estimated by the industry itself between 2000 and 2500 TCF. So the area under the red gas-generation curve represents between 35% and 44% of our geologic endowment.
879 TCF ÷ 2500 TCF = 35%. Using 2000 TCF yields 44%.
The 15.33 TCF consumed in 2015 for non-electricity uses would moderate through the 35-year duration as natural gas is displaced by WWS-derived electricity for space heating. It may decrease linearly to some baseline value required for fertilizer, plastics and fabrics. That is, we might perhaps approximate it as a straight line sloping down from 15.33 TCF /yr to perhaps one third that value, say 5 TCF /yr, as shown in Figure B.
Here is a deficiency. The proposed nameplate capacities of wind and solar in those four rows combine to only 5035.2 GW (expressed as 5,035,200 MW). That amount of generating capacity would not be sufficient to produce 1401 GW-y annually, when operating at the present US Capacity Factors - CF - for utility-scale wind and solar production devices.(objection) US wind & solar capacity factors were 29.7% for wind and 21.9% for utility solar in 2015.12
At those capacity factors the total annual energy produced by the Plan's standard-demand utility-scale wind and solar facilities (rows 1, 2, 9, and 10) would be:
For wind in rows 1 and 2: 737.1 GW-y per year. (0.297 CF X 2,481,900 MW combined capacity of rows 1 and 2)
For solar in rows 9 and 10: 559.2 GW-y per year. (0.219 CF X 2,553,300 MW combined capacity of rows 9 and 10)
Utility-scale wind and solar combined will produce 737.1 + 559.2 = about 1296 GW-y. Thus there is a production shortfall from the 1401 GW-y expected in the “Percent of 2050 all-purpose load” column.(objection) (1401 – 1296 = 105 GW-y shortfall)
Rooftop solar sources appear in rows 7 and 8. Residential rooftop is expected to produce 3.98% of the total standard load (column 2), which would be 0.0398 X 1591 = 63.3 GW-y.
Residential PV solar capacity at the end of 2015 was 5.53 GWac.12.3 Its potential production was 5.53 GW X 8760 h /yr = 48,440 GW-h. Residential solar’s actual energy production in 2015 was 6999 GW-h.12.4 Thus US residential rooftop solar operated at capacity factor = 14.4%. (6999 GW-h actual ÷ 48,440 GW-h potential = 0.144)
Residential solar CF is low because of south-siting issues, angle of tilt, and partial shading by trees and other buildings.
On row 7 of Table 2, the Plan’s eventual residential buildout to 379,500 MWdc will produce 322,600 MWac, operating at dc-to-ac conversion efficiency of 85%. [379,500 MWdc X 0.85 = 322,600 MWac] Look ahead to p. 10, Land Use Utility PV Solar , for discussion of the conversion efficiency of dc-to-ac inverters.
Therefore row 7’s residential equipment can be expected to produce yearly energy of 14.4% CF X 322,600 MW = 45.5 GW-y. Not 63.3 GW-y as that row’s column 2 percentage anticipates, for a residential PV shortfall of 17.8 GW-y.(objection) (63.3 – 45.5 = 17.8 GW-y)
Attending to commercial /government rooftop solar in Table 2’s row 8, the Plan expects to produce 3.24% X 1591 GW = 51.5 GW-y annually.
Commercial /governmental /industrial distributed PV solar capacity at the end of 2015 was 6.00 GWac.12.5 Its potential production was 6.00 GW X 8760 h /yr = 52,560 GW-h. Commercial distributed solar’s actual energy production in 2015 was 7140 GW-h.12.6 Thus US commercial rooftop solar operated at capacity factor = 13.6%. (7140 GW-h actual ÷ 52,560 GW-h potential = 0.136)
The Plan’s row 8 commercial buildout to 276,500 MWdc multiplied by 85% conversion efficiency will provide ac capacity = 235,000 MWac. At 2015’s capacity factor the equipment would therefore produce yearly energy of
13.6% CF X 235,000 MW = 32.0 GW-y. Not 51.5 GW-y as that row’s column 2 percentage anticipates, for a commercial PV shortfall of 19.5 GW-y.(objection)
(51.5 – 32.0 = 19.5 GW-y)
Summarizing, the combined wind & solar standard energy production of the Plan (rows 1, 2, 7, 8, 9, and 10), operating at 2015 capacity factors, would be 1296 + 45.5 + 32.0 = 1374 GW-y. Not 1516 GW-y, which the Plan expects. [1516 = 1401(rows 1, 2, 9 and 10) + 63.3(row 7) + 51.5(row 8)]
The few percent additional energy from hydroelectric and geothermal facilities (rows 3, 4, 5 and 6), amounts to only about 76 GW-y per year, taken from the percentages stated in that column. That is to say, 4.77% of 1591 GW-y is about 76 GW-y. Thus hydro and geo would boost the overall national total to only 1450 GW-y per year. [1374 + 76 = 1450 GW-y /year]
As presented, the Plan therefore has insufficient wind and solar infrastructure to achieve its standard-demand production target of 1591 GW-y /year, when operating at the US capacity factors prevailing in 2015.(objection)
It may be that the Plan's authors are hoping for equipment-driven or weather-driven capacity factor improvements in the coming decades. That may be a reasonable hope for turbine-blade technology advancement and by benefitting from very windy offshore placement of turbines. But onshore weather conditions are likely to be countervailing due to lower wind speeds as earth’s atmosphere warms.
It would also be reasonable to expect US utility-scale solar capacity factor to be enhanced by aggressively concentrating new farms in our southern states, especially our southwest deserts and Florida. But that doesn’t seem to be the Plan’s intent, referring to The Solutions Project Infographics for the 50 states.12.8 Those infographics seem to indicate that the states’ equipment mix dedicates an amount between 32% and 42% of the nation’s standard-demand solar facilities to the northern belt consisting of New York, New Jersey, Pennsylvania, Ohio, Indiana, Illinois, Michigan, and Wisconsin.12.9
Even by counting reserve peaking CSP from row 11, its additional energy capability does not nearly make up for Table 2's standard equipment deficiency. With nameplate capacity of 136.4 GWp (“Name-plate capacity” column 3 heading), and assuming a very generous solar insolation capacity factor of 27%*, the Plan’s annual peaking energy production from CSP would be only 0.27 X 136.4 GW-y = 37 GW-y /year.
*Contingent on CSP placement in very sunny regions only.
Combined with 1374 GW-y stated above from standard-demand sources in rows 1 through 10, that peaking addition gives 37 GW-y + 1374 GW-y =
1411 GW-y /year. So total US electric energy production (standard plus peaking backup) would still be about 180 GW-y less than the 1591 GW-y consumption value anticipated in 2050. In other words, not only does the Plan provide zero standard overbuild, it yields a significant energy shortfall even with its backup /storage factored in.
This is not credible. The Plan's electricity infrastructure's energy content is proposed to be substantially greater than for our electric grid of 2015. Namely 1591 GW-y, up from 1167 Gw-y in 2015, and it anticipates getting 97% of that substantially greater amount from unreliable sources. Yet it reduces our 2.5 X overbuild factor in 2015 down to no overbuild at all. As presently structured, it cannot succeed.
Later, this study will suggest a reasonable overbuild factor, after first performing a detailed analysis of the Plan’s material usage and costs. That overbuild suggestion will be considerably larger than 2.3 X. It seems indisputable to the author that such an increase in overbuild will be necessary to compensate for changing the character of our energy sources from always-on performance to intermittent performance.
Setting aside the overbuild issue for the time being, let us consider a possible build-out schedule for only that inadequate equipment which is proposed in Table 2. Given the 35-year duration, it is not possible to attack the build-out challenge in a linear fashion, by building 1 /35 of that equipment in the very first year, say 2016. There is not sufficient wind-turbine manufacturing capacity in the entire world to build 1 /35 of 484,200 turbines in a single year (rows 1 and 2 of Table 2, column headed “number of new plants or devices”). That would call for 484,200 ÷ 35 = 13,800 turbines, each one a 5-MW behemoth, to be built in a single year.
Our best-ever year for wind construction was 2012, when we added 13.1 GWp.13 At 5 MW per turbine, as called for in the Plan, year 2012 achieved the equivalent of 2620 such giant turbines. [13.1e9 Wp ÷ 5e6 Wp = 2620 turbines] Thus the 13,800 turbines that would be needed to jump off to a linear beginning would be 5.3 X greater than our all-time best year. That's impossible.
[13,800 turbines ÷ 2620 turbines = 5.3]
Even more so for solar panels. 2015 was our best year ever, with 6200 MWp-ac of new capacity installed.14 But 1 /35 of 2,982,000 MWp (rows 7, 8 and 9 combined from Table 2) would require 85,200 MWp to be constructed in the first year. [2,982,000 ÷ 35 = 85,200 MWp] Such a factor-of-13 jump would be even more impossible than the factor of 5.3 for wind. [85,200 MWp ÷ 6200 MWp = 13.7]
To tackle the Plan’s building project we would need to begin with the manufacturing capacity that we now possess, then continually construct more manufacturing plants year after year.
If the inertia afflicting American society could be overcome, the jealous withholding of material and financial resources and the paralysis of political will, it would in principle be possible to increase turbine and solar panel production exponentially. The phrase “increase exponentially” means to achieve an annual growth rate, some percentage, that compounds year-by-year.
Let us carefully consider that task for the wind buildout proposed in Table 2.
a) Onshore wind plus offshore wind is intended to produce 50.0% (add rows 1 and 2) of US average load for year 2050, which is 1591 gigawatt-years per year (bottom row of Table 1, referenced above). Thus 0.50 X 1591 = 796 GW-y, generated in the year 2050.
b) In 2015 actual US wind energy production was 21.8 GW-y.15 This is the initial value from which we would start compounding.
c) To grow at a compounded rate that boosts 21.8 to 796 GW-y /year would require an annual growth rate of 10.826%. Which implies a factor of increase equal to 1.10826, exponentially compounded. 21.8 X (1.10826)35 = 21.8 X 36.51 = 796 GW-y.
This exponential growth curve of wind energy is the blue line in the Figure A graph.
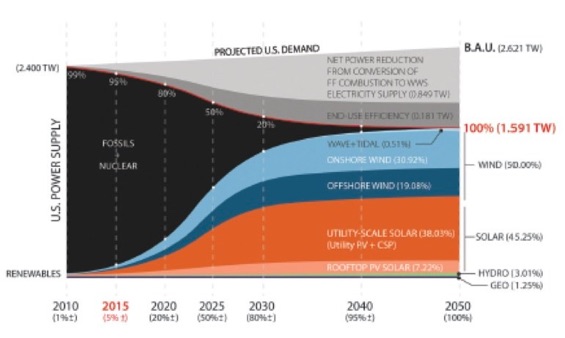
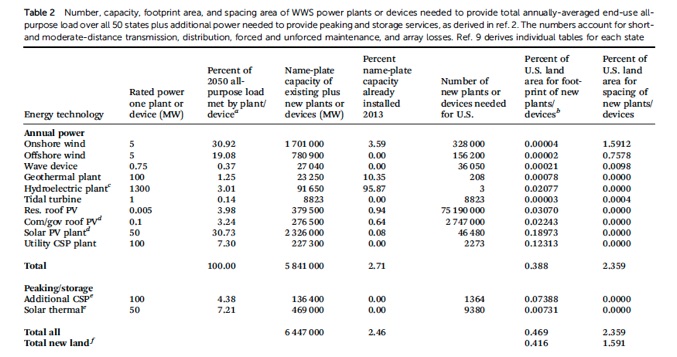
7.5 megawatt wind turbine
200-meter hub height
wind farm in UK
If I've heard it once, I've heard it 20 times. "Jacobson has shown that we can power the electric grid totally with renewables", or words to that effect.
That idea comes up at every conference, Sierra Club meeting, Q&A session after a presentation, or what have you. It's reassuring to people who are concerned about the environment, so they cling to it. "Jacobson says…"
Jacobson has now gone them one better - that we can run our entire society, not just the present electric portion of it, totally with renewables. I'm not sure that conceptual leap has sunk in with the environmental community. It's not just lights, TVs and toasters anymore. Now it’s cars and trucks, space heating /cooling, and all commercial /industrial activity including heavy manufacturing – our entire Primary Energy consumption.
The catch-phrase is "100% Renewable Energy Vision" and the scholarly paper is titled 100% Clean and Renewable Wind, Water, and Sunlight (WWS) All-Sector Energy Roadmaps For the 50 United States, published in 2015. The scholarly paper's shorthand designation is the 100% WWS Plan.
I've gone through the 100% WWS Plan at some length, and here's my critique of it. Spoiler alert: The amount of land that it needs is vast; the amounts of money and material are enormous beyond your wildest dreams; and it won't work.
A critique of the paper 100% clean and renewable wind, water, and sunlight (WWS) all-sector energy roadmaps for the 50 United States, by Mark Jacobson et al
A critique of the paper 100% clean and renewable wind, water, and sunlight (WWS) all-sector energy roadmaps for the 50 United States,
by Mark Jacobson, Mark Delucchi, et al,
published in Energy and Environmental Science, 2015, 8, 2093.
Abstract
The Solutions Project is an environmental organization that believes all the world's energy for the functioning of modern industrialized societies can be obtained from five renewable sources: solar, wind, conventional hydroelectric, wave /tidal hydro, and geothermal. It intends stopping the burning of all fossil fuels - coal, oil, and natural gas - and also seeks the phase-out of nuclear fission energy.
Its website at thesolutionsproject.org advances a plan to accomplish this goal for the United States by year 2050, using a localized mix of energy sources for each of the 50 states. The plan is titled 100% Renewable Energy Vision for the United States of America.1
The most public face of The Solutions Project is Mark Jacobson, professor at Stanford University and head of its Atmosphere and Energy Program who, in 2009 with professor Mark Delucchi of University of California, published a watershed article in Scientific American titled A Path to Sustainable Energy by 2030.2
From that publishing event, and especially since the founding of The Solutions Project in 2011, it has become the mantra of wind, water, and solar energy proponents - WWS - that "Jacobson says that it can be done".
In 2015 Jacobson, Delucchi, et al published in the journal Energy and Environmental Science a lengthy paper titled 100% Clean and Renewable Wind, Water, and Sunlight (WWS) All-Sector Energy Roadmaps For the 50 United States.3 It has become the go-to document for WWS adherents in discussions of future US energy policy. I will refer to this paper as the 100% WWS Plan, or simply the Plan.
The intention of this critique article is to present a careful analysis of the 100% WWS Plan in terms of certain technical characteristics and specifications of wind energy and solar energy. It will also judge the reasonableness of the proposed wind and solar construction schedule.
The analysis will quantify four aspects of each energy source that is advocated by the Plan. Those four aspects are:
A) Steel and concrete used
B) CO2 emitted during construction
C) Land required
D) Dollar cost
The quantified energy sources are:
1. Utility-scale photovoltaic - PV - solar
2. Residential rooftop PV solar
3. Commercial /governmental rooftop PV solar
4. Onshore wind
5. Offshore wind
6. Concentrated thermal solar - CSP - with molten-salt energy storage
Each of the six sources is treated in terms of its amount specified by the Plan. All six energy sources will then be summed to specify material and land use, CO2, and dollar cost for the entire 35-year Plan buildout.
he analysis disputes several numeric values stated within the Plan, especially in regard to land areas occupied by wind and solar equipment. Objections also are registered to other issues that are numerically quantified. Those include energy amounts, capacity factors, graph scaling, and overbuild assumptions. All such instances can be located within this article by searching the word “objection”.
It is explained why the Plan's anticipated time schedule is unachievable, and the article presents an alternative 35-year-duration time schedule that could be regarded as feasible.
It calls attention to the enormous increase in natural gas consumption that would be required during the 35-year construction. With that cumulative consumption shown to have an existential effect on our nation's recoverable reserves after year 2050.
It disputes one of the 100% WWS Plan's assertions, which derives from its mathematical modeling of the years 2050 – 2056 by the LOADMATCH program.4 Namely the assertion that in the post-2050 future we will no longer need overbuild of our electric-generating capacity. That is to say, our past and present arrangement of the electric grid, which maintains excess generating capacity greater than our summer peak demand, can be done away with. That overbuild has historically provided a "cushion" or "buffer" which has contributed to maintaining electric service about 99.9% of the time.
Regarding this issue the present critique espouses the opposite, arguing that the overbuild buffer would need to be increased if we were to make the switch from always-on baseload-type sources to intermittent wind and solar sources. And that the amount of necessary overbuild would cause the Plan's already huge construction undertaking to become enormous beyond imagination.
For comparison to the 100% WWS program, this article will perform an analysis for steel and concrete material, CO2 emissions, land, and dollar cost for Generation 3+ nuclear fission, based specifically on the Westinghouse /Toshiba model AP10005 pressurized water reactor. That AP1000 analysis reveals an impressive reduction in material use and CO2 emissions, a spectacular advantage in land area required, and a substantial dollar cost savings.
To view the nuclear versus WWS comparison result immediately, perform a search for “Gen 3+ Nuclear plan”.
The nuclear-to-WWS comparison is followed by a brief discussion of the advantages to be derived by development and installation of small modular reactors using the same technology features offered in the large model AP1000.
Finally, the article looks forward to Generation 4 reactors, specifically the Molten Salt Reactor. MSR is a technology that has not yet been commercialized, but which is under development by at least four American companies,6 a Canadian company7 and by a Chinese Academy of Sciences R&D program.8 An overview is presented of MSR’s expected safety character, heavy-atom waste reduction, long-term fuel supply, and likely cost.

100% WWS Plan
The Solutions Project 100% WWS plan - "the Plan" - undertakes not just to provide 100% of US electricity from renewable sources, but to provide the entire US Primary Energy supply. PRI NRG encompasses
A) Electricity;
B) Transportation - now mostly gasoline and diesel from petroleum;
C) Space heating for residences and commercial buildings - now mostly natural gas, with some heating oil; and
D) Industrial process heat - now from natural gas, petroleum and coal.
Those four sectors partition our Primary Energy consumption in this way: A) Electricity = 39%; B) Transportation = 28%; C) Space Heating = 11%;
D) Industrial Processes = 22%.
To operate just the 39% of electricity, we have constructed a generating /transmission infrastructure that has a maximum energy-production capability, often called peak generating capacity, more than 2 X greater than our average demand. Specifically, we have put in place 1167 gigawatts9 of peak generating capacity, a factor 2.5 X greater than our US average demand of 467 GW10 in 2015.
Furthermore, that 1167 GW is 1.52 X greater than our nation's summer peak demand of 768 GW.11
This overbuild, to call it by that term, is necessary in order to guarantee that the electric power is almost always on, everywhere. Overbuild is required even now, when most of our generating facilities are themselves non-intermittent. Coal, natural gas, and nuclear plants, which together supply 85% of our electric energy, are always available unless they are shut down for maintenance or refueling. Even given their always-on nature, we still must overbuild them in order to achieve the flexibility to share electric energy among geographic regions at different seasons and times of day.
In order to have any chance of success at satisfying our entire 2050 PRI NRG consumption, which is a far more ambitious goal than the present-day 39% electricity portion, the Solutions Project Plan should include an overbuild factor substantially greater than 2.3 X . That's because most of its electric supply is to come from intermittent wind and solar sources, rather than 85% from always-on sources, as we presently have.
However, such an increased factor of overbuild is not called for by the Plan.(objection)
Table 1 on p. 7 anticipates 1591 GW-y total all-purpose load in year 2050. In Table 2 on p. 8, referring to the column headed “Percent of 2050 all-purpose load”, the regular-demand electric plants in rows 1 through 10 are shown combining to produce 100% of that anticipated 1591 GW-y.




Table 2 of the 100% WWS Plan.
Page 6 of the published study; frame No. 8 of its PDF document.
https://web.stanford.edu/group/efmh/jacobson/Articles/I/USStatesWWS.pdf
parabolic-trough CSP
reflector-mirror
PV solar panels swarm
California hillside
Figure A
Various energy sources during the 100% WWS Plan’s 35-year build-out.
The building schedules for wind and solar are here presumed to be exponential.
The natural gas-for-electricity red curve accounts for hydro’s contribution.
That red curve can be graphically integrated to find cumulative natural gas consumption through year 2050.
Mr. Todd De Ryck has been kind to reconstruct this web page using WordPress.
In that form it may be more sharable. It can be seen at
https://thstlewpg.wordpress.com/2016/09/17/tim-maloneys-analysis-and-critique-of-100-wws-for-usa/
To achieve such a schedule, we would need to prodigiously expand our manufacturing capacity for PV panels and for wind turbines by year 2020. Is that feasible?
To address this question, let us quantify the build-out rate represented in Figure 5 for the 2020–2025 period. Then we can compare that hoped-for build-rate to what has been accomplished so far, to 2015.
Before beginning this task, we must register an objection to Figure 5 regarding its vertical scale value 2.400 TW for US Power Supply ("end-use power demand for all purposes" in the figure caption). That 2.400 value would imply US annual PRI NRG of 2400 GW-y for year 2010.
But actual US PRI NRG for 2010 was 3261 GW-y, per the Energy Information Administration - EIA. They state 2010’s PRI NRG as 97.48 quadrillion BTU's,51 called Quads. With conversion factor 1 Quad = 33.456 GW-y, we actually consumed 97.48 Q X 33.456 GW-y /Q = 3261 GW-y.
Thus the correct PRI NRG values pertaining to the US for years 2010–2050 would be greater than the values shown in Figure 5, by a factor of 1.36. [3261 GW-y ÷ 2400 GW-y = 1.36] We will deal with this error by obtaining graphical scaled values from Figure 5 as it is presented, then multiplying all such results X 1.36 to represent our country’s reality.
There are six data points that must be extracted from Figure 5 to enable calculation of build-rates for solar and wind during the 2020–2025 period. They are:
Data Point (1): The bottom point of the orange regions at year 2020. This point represents the tiny bit of PRI NRG supplied by hydro and geothermal in 2020, to which the orange solar regions add their contributions. That value cannot be scaled because it's so tiny, but we can estimate it as about 1.5% of US PRI NRG because we know from EIA that hydro plus geothermal contributed 0.9% in 201052 and in 2015.53 We will suppose that 2015’s contribution of 0.9% can grow to about 1.5% by year 2020 (though hydro has been decreasing lately).54
Thus, in Figure 5 we will call the value at the bottom of the orange region as 0.015 X 2400 GW-y = 36 GW-y.
Data Point (2): The top point of the orange solar regions at year 2020, which is also the bottom point of the blue wind regions. This value, with 36 GW-y subtracted from it, represents the PV and CSP solar contribution to US PRI NRG during the year 2020 (before adjustment X 1.36, as for all graphical data points that we extract).
This data point (2) also lays the basis for finding the contribution made by wind in the year 2020.
Data Point (3): The top point of the blue regions at year 2020. This value, with the bottom point of the blue regions subtracted from it (Data Point No. (2) represents the wind contribution in year 2020.
Data Point (4): The bottom of the orange regions at year 2025.
Data Point (5): The top of the orange, bottom of the blue regions, at year 2025.
Data Point (6): The top of the blue regions at year 2025.
Performing mechanical ruler scaling at points 2 and 3, and at points 5 and 6, we obtain:
Point (2): 254 GW-y extracted graphically
Point (3): 449 GW “
Point (5): 566 GW-y “
Point (6): 1034 GW-y “
Data Point (4)’s value also is too tiny to be scaled. We will estimate it very optimistically as 2.0% of 2010’s PRI NRG, so 0.02 X 2400 GW-y = 48 GW-y.
Data Points (2), (3), (5) and (6) taken from Figure 5 must be corrected to actual US PRI NRG values by multiplying X 1.36. We obtain
Point (2): 345 GW-y corrected X 1.36
Point (3): 611 GW-y “
Point (5): 770 GW-y “
Point (6): 1406 GW-y “
Data Points (1) and (4), 36 GW-y and 48 GW-y, are valid as stated above because they were not obtained from erroneous graph-scaling.
We thus conclude the following quantities conveyed by the Plan's S-shaped building schedule.
For year 2020:
Solar contribution to PRI NRG would be 309 GW-y. [345 – 36 = 309] [corrected Point (2) minus Point (1)]
Wind contribution to PRI NRG would be 266 GW-y. [611 – 345 = 266] [corrected Point (3) minus corrected Point (2)]
For year 2025:
Solar contribution = 722 GW-y. [770 – 48 = 722] [corrected Point (5) minus Point (4)] [represented by width of expanded orange regions]
Wind contribution = 636 GW-y. [1406 – 770 = 636] [corrected Point (6) minus corrected Point (5)] [represented by width of expanded blue regions]
So by careful use of the Figure 5 graph, we find for the 5-year period 2020– 2025:
The building rate for solar would have to be [722 GW-y (in 2025) minus
309 GW-y (in 2020)] ÷ 5 yr = 82.6 GW-y /year for solar, obtained graphically.
The building rate for wind would have to be [636 GW-y (in 2025) minus
266 GW-y (in 2020)] ÷ 5 yr = 74.0 GW-y /year for wind, obtained graphically.
Throughout the above derivation we have accepted the relative widths of orange to blue as properly drawn in the early part of the build-out (years 2020 – 2025). We have done so despite their being improperly drawn(objection) for year 2050. Orange is drawn wider than blue at 2050, though producing less energy. That is, orange PV and CSP solar produces only 45%, versus blue wind's production of 50%. (Refer to “Percent of 2050 all-purpose load met by plant /device” in Table 2.) Therefore blue should be drawn wider than orange.
The building rates extracted above from Figure 5's S-curve have been interpreted in Energy units (GW-y). That is equivalent, in purport, to interpreting in Average Power units (gigawatts average, symbolized GWavg, strictly speaking).
However, renewables build-out rates are almost always denoted in peak units, symbolized GWp, strictly speaking. Usually verbalized as "peak capacity" or just "capacity".
To render a nation's energy units (equivalent, in purport, to a nation’s average power) into the nation's peak capacity units, we must know the nation's average capacity factor CF for that particular technology.
For the US in year 2015, per EIA and Solar Energy Industry Association - SEIA - average capacity factors were:
PV (all 3 placements) and CSP solar: 18.3%55
Wind: 29.7%56
Total solar CF was mediocre because low-CF residential and commercial distributed solar are still a substantial portion of the US capacity in 2015. Utility-scale systems, with their proper south-facing panel orientation, would far surpass residential and commercial capacity in the Plan's implementation. Well situated PV and CSP utility farms can achieve insolation capacity factor percentages in the low-twenties (mid-twenties in southwest US).
We will assume 23% CF as the expected nationwide average for our aggregate solar equipment after year 2020. That value is appropriate for large-project PV solar's ac peak capacity, and for large-project CSP’s entire solar-field insolation energy (eschewing the artificially reduced /restricted solar-field energy that is usually published).
New wind installations perform better than the average of the entire US wind fleet, which naturally contains many older, smaller machines. The American Wind Energy Association - AWEA - and the US DOE have put forward a
32% – 35% range of capacity factors expected for new wind farms.57 For discussion purposes we will assign the value 33.5% from the middle of that range.
With those two capacity factor assumptions, 0.23 solar and 0.335 wind, expected for the 2020–2025 building period, and referring to the graphically obtained solar and wind building rates expressed in energy units above, the required annual rates of peak capacity construction become:
Solar: 82.6 GW-y /year ÷ 0.23 = 359 GWp-ac /year
Wind: 74.0 GW-y /year ÷ 0.335 = 221 GWp-ac /year
2016 was our best-ever year for PV solar installation with 14.63 GWp-dc added,14 implying about 12.43 GWp-ac with conversion efficiency of 85%. Therefore the 100% WWS Plan intends to ramp up our solar panel manufacturing capacity (or China's) from 12.43 GW to 359 GW, a factor of 29X, within the next 5 to 10 years. This is not credible. (objection)
For wind, 2012 was our best year ever, with 13.1 GWp added.13 This means that the Plan's authors intend to simultaneously ramp up somebody's wind turbine manufacturing capacity from 13.1 GW to 221 GW, a factor of 16.9, also within 5 to 10 years. Not as preposterous as solar, but still not credible. (objection)
Perhaps the 100% WWS Plan’s wind ambition can be best appreciated by specifying individual wind towers /turbines. Taking the Plan's 5-MW per machine, 2012 saw the equivalent of 2620 such turbines built in the US. [13.1 GW ÷ 5 MW = 2620] By 2020 – 2025 that installation rate would need to increase to 16.9 X 2620 = 44,300 turbines per year.
Can anyone credit 44,300 gigantic wind turbines manufactured and installed in one year? 69% of them must find a home on land (refer to Table 2, rows 1 and 2). That would require about 30,600 towers per year moving onto about 25,900 km2 (10,000 sq mi) of land. [221 GW X 0.69onshore X 0.17 km2 /MW = 25,900 km2] By the end of the proposed 5-year building binge they will have covered half of Kansas. [5 X 10,000 sq mi per year = 50,000 sq mi] Plus new electric transmission lines to carry their product.
From the land-acquisition perspective, these wind towers are even more extravagant then the Plan's solar ambition.
Forget the S-shaped building schedule portrayed in Figure 5. It's utterly impossible. (objection)
As was urged at the beginning of this critique, if we are obliged to take the Plan's goals seriously, we must organize a building schedule that keeps compounding its annual production through all 35 years. That way, the greatest annual installations occur in years 2049 and 2050.
Then we suddenly quit. Maybe we can use our newly acquired manufacturing facilities to produce for the export market. That could be a solution to our problem of factory off-shoring.
Let us return to Figure A and repeat its description. Its building curve is strictly exponential, with every year’s new manufacturing capacity compounding the previous year’s manufacturing capacity, by some percentage, year-after-year. It lacks the graceful appearance of Figure 5, but that’s not its chief unpleasantness. Its chief unpleasantness is that it denies the Pollyanism of expecting to get most of the building job finished quickly. It’s disappointing, but it's the only remotely sensible approach.
The Overbuild Issue
At this point in the discussion, here's where we stand concerning the proposed 100% WWS Plan.
1) We will cover South Carolina with solar panels. {Or perhaps only Massachusetts, Connecticut and Rhode Island per NREL’s packing factor approach in future}
2) We will fill up Kansas, West Virginia, and half of Vermont with wind farms.
3) We’ll clutter up our coastal waters with a half-Florida’s worth of wind farms.
4) We'll burn up nearly half of our natural gas endowment. (Never mind those anti-fracking initiatives.)
5) We'll increase modestly our already-shameful CO2 and GHG emissions.
6) We're on the hook for 16-or-so trillion dollars.
That No. 6 item is about 30 X what the Interstate Highway System cost,58 measured in today's dollars. Not that money should be our main concern. Whatever it takes, when human civilization is on the line.
Maybe all this would be tolerable if it really worked. But it wouldn't work, (objection) because it contains only 4% “overbuild”, claimed /admitted in row 11 of Table 2.
The Plan’s authors assure us that a grid-integration analysis performed by them for year 2050, that uses wind and solar time-series data from a
3-dimensional global weather model, and which incorporates demand response (including some automatic use-restrictions), predicts that substantial overbuild will not be necessary in the future. The grid-integration mathematical model is cleverly named LOADMATCH.59
The model incorporates anticipated load (demand) information at 30-second intervals for a six-year period beginning in 2050. It does the same for wind and solar resource availability. That is, both supply and demand are antici-pated for every 30 seconds throughout the six-year period 2050 through 2055.
Their grid-integration strategy intends using some energy-storage technologies that are already well-established, pumped hydro being foremost. It intends also using some technologies that have not been demonstrated at scale, portable hydrogen derived from water electrolysis being the prime example.
Here are some few observations about the LOADMATCH grid-integration study that seem relevant to this author.
1) Planetary climate and weather conditions that will prevail 35 years from now cannot be known with any confidence. Altered wind patterns are the most striking possibility. Availability of water for pumped-hydro energy storage to back up PV solar and wind farms in dry regions is another dubious assumption.
2) Is underground thermal energy storage in soil - UTES - which the LOADMATCH study expects to use for air- and water-heating, applicable to urban population centers? How deep and wide will we have to dig within our large cities in order to access enough soil volume to hold sufficient heat for those applications in order to serve a population of several million? Can such excavation and installation really be carried out beneath a modern city, with its water and gas pipes, sewers, and wire & cable trays?
3) Can hydrogen ever be made safe for commercial and personal transportation? The H2 molecule leaks like mad and it's explosive.
4) Will our citizenry cooperate with demand-response restrictions affecting their lifestyles? Suppose we put it that household refrigerators won't be able to run from 5 PM to 8 PM. Will folks adapt to that by keeping the fridge door closed, or will they try to defeat the controller?
What we know for sure is that the age of electrification has always needed excess generating capability to feed the electric grid, in order to ensure that the power is almost always on for everybody. This is the meaning of the concept overbuild. Embarking on a total reorganization of our society’s PRI NRG infrastructure, under the expectation that we won’t need excess power-generating capability in the future, seems a grossly imprudent risk.
In our present arrangement the electric grid is responsible only for running electrical appliances – lights, refrigeration, cooking stoves, televisions, pumps at water-treatment plants, etc. We don't expect it to run our vehicles, or to heat our buildings (except for air-blowing through ducts), or to run our industrial heat processes (except for electric-arc furnaces and suchlike).
But the 100% WWS Plan changes that arrangement. It does expect the electric grid to take over all those other necessities of modern living. Instead of our electric grid taking just 39% of PRI NRG consumption, now the grid will take the entire 100% of society’s PRI NRG.
Not only would the electricity sector be swallowing all of the energy that we can acquire, but also the sources from which we acquire the energy won’t be always functioning. That is a basic conceptual difference from coal, natural gas, nuclear, or conventional hydro. If one visits a coal plant, there is always a big pile of coal on the site; for a natural gas combustion turbine, the gas pipe is always pressurized; for a nuclear plant there is always plenty of unfissioned uranium present within the fuel-rods; for Hoover Dam there is always water in Lake Mead. At least we hope so.
The WWS scenario must cope with windmills that might not have wind, so won’t be spinning. Solar panels certainly don't work at night, but they also don't work very well on cloudy days. Even ocean wave action isn't totally reliable.
With both of these two altered conditions, namely a) expanded duties, and
b) sources sometimes not working, is it reasonable to put confidence in a future-decades mathematical model prediction that claims we will no longer require overbuild? It doesn’t seem reasonable to me.
USA's present electrical overbuild factor is 2.5. That's the ratio of our maximum annual electric energy production capability (if all generating sources were able to produce at their peak capacity for 100% of the time), relative to our actual annual energy consumption.
Actual annual energy consumption is in purport equivalent to our average power demand, or power “consumption”.
Our 2015 maximum annual electric energy production capability is
1167 GW-y.9 That production capability is partitioned below by fuel type. Our actual electric energy consumption was 467 GW-y10 (our average power demand was 467 GW). Overbuild factor is thus 1167 GW ÷ 467 GW = 2.50.
[The concept of maximum annual energy production capability is usually referred to as "peak capacity", regrettably. Using that expression invites confusion between A) "peak" in the sense that we could, if we chose at our discretion, adjust the output from every last one of our generators to its maximum value; versus B) "peak" in the sense of conditions being momentarily felicitous for good production activity (luckily, the wind happens to be blowing briskly, for example).]
Accepting the 51%-CF nameplate peak goals in rows 10 and 11 of Table 2, we have 363,700 megawatts peak-ac, as noted earlier. At $5.94 /Wp that would run us 2.2 trillion dollars. [$5.94 X 363,700e6 = $2.16e12]
It’s nearly the same amount that we would be spending on residential PV, but CSP gives us a lot more energy for our money. Namely 186 GW-y /year versus residential's 63 GW-y /year.
It should be mentioned that the $5.94 /Wp cost figure is a big improvement over the unit cost to build Andasol just a few years ago. Andasol did cost about $1.2 billion,47 assuming a conversion rate $1.30 per Euro. Its nameplate capacity is 150 MWp, so it was built at a unit cost of $8.00 /Wp, not long ago. [$1.2e9 ÷ 150e6 W = $8.00 /Wp]
Summarizing the Plan's proposed CSP build-out, we have: CSP Solar
Land: 19,200 km2, the area of New Jersey
Material and CO2: 188 million t steel; 605 million t steel; 1060 million t CO2
Money: $2.2 trillion
Sunlight is free and mirrors don’t degrade very rapidly, so that expenditure is supposed to provide 11.7% of our primary energy for a lifetime.
Total W&S build-out cost:
Relying on US government and industry association sources of information, we conclude that the Plan’s 35-year construction of wind and solar facilities would entail a cost of $15.2 trillion. [all 3 PV solars + combined wind + CSP solar = $7.7 T + $5.3 T +$2.2 T = 15.2 T] 100% WWS Plan - entire
US electric production capabilities
(usually expressed as "peak capacities”)
By fuel type60
Expressed in power units - GWp.*
Natural gas: 503.9 GWp
Coal: 304.8 “
Nuclear: 103.9 “
Dammed hydro: 79.0 “
Wind: 73.4 “
Petroleum: 42.3 “
Pumped hydro - PHES 21.6 “
Solar:** 13.8 “
Biomass, methane, other: 10.7 “
Wood fuels: 10.2 “
Geothermal: 3.8 “
Total: 1167 GWp
Always-on technologies, combined: 1080 GWp
(includes PHES, bio and geo)
Intermittent technologies, combined: 87.2 GWp
(wind & solar**)
* May also be expressed in energy units of gigawatt-years, GW-y, adopting the unrealistic assumption that all generators operate at 100% of maximum output, all the time.
(As a general aid for rationalizing confounding statements involving the words "energy" and "power", feel free to mentally insert the words "per 1 second” with regard to energy; or "multiplied by 1 second" with regard to power.)
**Utility-scale only. Not counting distributed (rooftop), with 11.5 GWp-ac capacity.
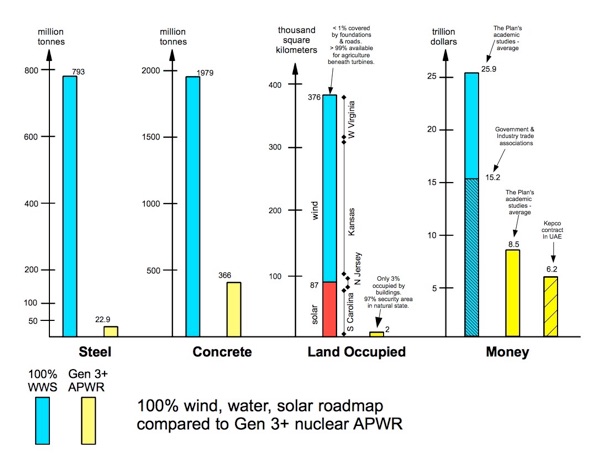
If we discover through the years that we must maintain our national overbuild ratio at its present 2.5 X value in order to ensure always-on status for everybody and everything in our entire primary energy economy, then all nuclear use-figures will rise by that same factor because we'll need to build
2.5 X 1376 = 3440 reactors.
At $6.2 B apiece, we would pay 3440 X $6.2 B = $21.3 trillion. A huge amount to be sure, but better than the $60 trillion that we were staring at with my 4 X estimated overbuild of intermittent renewables.
Besides, aren't we hoping to install distributed SMRs in individual neighborhoods? Power to the people, as it were. No more long-distance sharing of dispatchable power among various geographic regions.
If that distributed local generation plan becomes our national model, we'll very likely be able to reduce our overbuild factor to less than its present 2.5 X. In that situation we can expect some savings on the $21.3 trillion expenditure in the paragraph above.
Keep in mind, Generation 3+ nuclear reactors by Westinghouse are not a futuristic technology like hydrogen-fueled transportation, for example. The first AP1000 reactor at Sanmen has finished construction and is now undergoing reduced-temperature testing of its piping systems. It's expected to begin generating power in 2017.69
Gen 3+ small modular reactors are technologically the same as full-scale AP1000s . There is no technical barrier to their integration into our energy system at a fraction of the cost of the 100% WWS Plan. And no problem finding room to put them.
What About Generation 4
Molten-Salt Reactors - MSRs?
Sure, let's get cracking on them. The scientific proof-of-concept has been demonstrated in the 1960s at Oak Ridge National Laboratory - ORNL.70
The fuel, thorium, is cheap and inexhaustible. It makes up 13 parts per billion of the entire Earth crust.
An MSR can't melt down because the fuel is already liquid. It can't suffer a steam- or hydrogen-explosion because it doesn't use any water, so there's no source of hydrogen.
Because it achieves 100% fissioning, "burn-up", of its fuel, an MSR doesn't produce any heavy-atom waste. That's quite unlike solid-fuel uranium reactors like the AP1000, which achieve only about 3% burn-up of their fissionable uranium. Their other 97% goes into spent-fuel storage. The only "waste" from an MSR is a small amount of non-fissionable radioactive medium-weight atoms, about 1 cubic foot volume per year of operation.71
MSRs are the ideal solution to the problem of what to do with unfissioned heavy atoms, uranium and plutonium, which are now sitting in cooling ponds inside spent fuel-rods. We can open those fuel-rods to extract the unfissioned uranium and plutonium, then feed those heavy atoms into an MSR, causing them to fission. As in, they won't exist anymore.
Radiation leakage? If MSR fuel ever leaked, which it won't because it operates at only atmospheric pressure, the liquid would just lie on the floor in a puddle until it cooled and solidified. It's not a gas, so it can't drift away into the atmosphere.
This technology will be inexpensive to build because it doesn't have:
a) high-pressure plumbing;
b) backup cooling pumps to remove decay heat if the chain-reaction ever stops, since the liquid fuel would simply flow by gravity into a dump tank where it will cool at its own leisurely rate until it solidifies;
c) stainless-steel pressure vessel to contain a hydrogen explosion and drifting gases (Fukushima event), since there's no hydrogen anywhere nearby;
d) steam condenser to convert turbine exhaust steam into liquid water in preparation for reheating for its next pass through the turbine. MSR won't use steam for its turbine fluid. It will instead use a high-temperature gas like helium.
So MSR is safe, cheap, eliminates other peoples’ radioactive waste, and comes with enough thorium fuel on the planet to last forever. What's not to like?
Dear 100% WWS advocates: thanks for your good intentions and for your bold attempt to change not just electricity, but our entire PRI NRG supply away from fossils. But let's skip the hassle of windmills and solar panels. The Thorium Energy Alliance has got a better idea.
Footnotes
For convenience, footnotes can also be viewed separately on adjacent webpage.
1. http://thesolutionsproject.org/
2. http://www.scientificamerican.com/article/a-path-to-sustainable-energy-by-2030/
https://web.stanford.edu/group/efmh/jacobson/Articles/I/sad1109Jaco5p.indd.pdf
3. https://web.stanford.edu/group/efmh/jacobson/Articles/I/USStatesWWS.pdf
The Plan
4. http://web.stanford.edu/group/efmh/jacobson/Articles/I/CombiningRenew/CONUSGridIntegration.pdf
Low-cost solution to the grid reliability problem with 100% penetration of intermittent wind, water, and solar for all purposes, pages 1, 2, 4
5. http://me1065.wikidot.com/ap1000
http://www.transatomicpower.com/
7. http://terrestrialenergy.com/
8. http://energyfromthorium.com/2011/01/30/china-initiates-tmsr/
https://www.technologyreview.com/s/542526/china-details-next-gen-nuclear-reactor-program/
9. http://search.usa.gov/search?utf8=%E2%9C%93&affiliate=eia.doe.gov&query=existcapacity_annual.xls
Then click or copy & paste first [XLS] www.eia.gov into browser; Open or Save the offered file; a spreadsheet doc will come up; scroll to line 38851 year 2015, All Sources, Nameplate Capacity 1,167,365 (1167 GW); Summer Capacity 1,064,054 megawatts (1064 GW)
Alternatively, copy and paste into browser
US nameplate & summer electric capacity - all sources code H37306 line 37065.xls
Click Combined Heat and Power link; Open or Save the offered file; that same spreadsheet doc will come up; scroll to line 38851
All Sources total is followed by other energy sources used by Electric Power Industry: Coal, Geothermal, Hydro (conventional dammed), Natural Gas, Nuclear, combine Other Biomass with Wood and Wood-Derived Fuels, Petroleum, Pumped hydro energy storage - PHES, Solar Thermal and Photovoltaic are lumped together, Wind.
US wind capacity at end of 2015 was 73.4 GW; line 38863;
after 2015 addition of 8.6 GW.
US utility-scale solar capacity, PV and CSP combined, at end of 2015 was 13.76 GWac; line 38862;
after 2015 addition of 6.2 GWac
10. http://www.eia.gov/totalenergy/data/monthly/pdf/sec7_5.pdf
Table 7.2a, 2015, total = 4,087,381e6 kW-h; 4087.4e12 Wh ÷ 8760 hr /yr = 466.6e9 W-y, 467 GW-y
11. http://www.eia.gov/electricity/annual/html/epa_08_06_a.html
Table 8.6.A, 2012, contiguous US = 767,762 megawatts
12. http://www.eia.gov/totalenergy/data/monthly/pdf/sec7_5.pdf
for 2015:
utility-scale solar actual NRG = 26,473 GW-h (PV and CSP);
utility solar capacity (PV and CSP) = 13.76 GWp (footnote No. 9);
utility solar NRG potential = 13.76 GW X 8760 hr /yr = 120,500 GW-h;
utility solar CF = 26,473 GW-h ÷ 120,500 GW-h = 21.9%
wind actual NRG = 190,927 GW-h;
wind capacity = 73.4 GWp (footnote No. 9);
wind NRG potential = 73.4 GW X 8760 hr /yr = 643,000 GW-h;
wind CF = 190,927 GW-h ÷ 643,000 GW-h = 29.7%
12.3 www.seia.org/research-resources/solar-industry-data
p. 1; vertical axis scale factor is 61.1 MWac per mm; ruler-scale all green-color bar heights from 2005–2015, then add those eleven measurements to obtain 90.5 mm; multiply 90.5 mm X 61.1 MW /mm = 5530 MW or 5.53 GW capacity, residential placement
12.4. http://www.eia.gov/totalenergy/data/monthly/pdf/sec10_10.pdf
Table 10.6, row 2015 Total
Residential sector = 6999 GW-h;
12.5 Ibid. 12.3 www.seia.org/research-resources/solar-industry-data
p. 1; vertical axis scale factor is 61.1 MWac per mm; ruler-scale all red-color bar heights from 2005–2015, then add those eleven measurements to obtain 98.2 mm; multiply 98.2 mm X 61.1 MW /mm = 6000 MW or 6.00 GW capacity, commercial placement
12.6 Ibid. 12.4 http://www.eia.gov/totalenergy/data/monthly/pdf/sec10_10.pdf
Table 10.6, row 2015 Total, columns 2 and 3
Commercial + Industrial sectors = 5689 + 1451 = 7140 GW-h
12.8 www.thesolutionsproject.org/resource/50-state-visions-infographics/
Download 50states_PDFs_all ; open the folder named 50states_PDFs_all; double-click the pdf icons for those 8 states; record from each state’s graphic the percentages of that state’s total Primary Energy to be provided by 1) Solar PV plants, and 2) CSP plants.
Add these percentages to obtain utility solar’s contribution to that state’s Primary Energy (all 4 sectors - electric, transport, heating /cooling, industry)
12.9 Find each state’s Primary Energy consumption in year 2013 by entering in browser bar
https://knoema.com/atlas/United-States-of-America/New-York/Energy-consumption
Record the large-font number at upper-left which is New York’s PRI NRG in units of billions of BTUs. Move the decimal point 6 places to the left to express in units of quadrillion BTUs, called Quads, unit-symbol Q.
Multiply by the conversion factor 293 TWh /Q to convert to terawatt-hour units for Primary Energy.
Repeat this process 7 more times by replacing New-York with the other states’ names in the browser bar. New-Jersey is hyphenated.
Multiply each state’s 2013 Primary Energy by the following factors to obtain its estimated Primary Energy demand in year 2050, per Table 1 of the Plan (footnote 3).
NY = 0.636; NJ = 0.572; PA = 0.628; OH = 0.615; IN = 0.628; IL = 0.619; MI = 0.616; WI = 0.640.
Multiply each state’s estimated PRI NRG by the solar percentage obtained for it from the operation in footnote 12.8. That gives each state’s utility-scale solar-supplied energy in 2050 in TWh units.
Add all 8 states solar consumption to obtain 1709 TWh in year 2050. Divide 1709 TWh by 5300 TWh to obtain 32.2%.
The value 5300 TWh is obtained from the Plan’s Table 2 by adding column 2 in rows 9 and 10 to get 38.03%, then multiplying 38.03% X 13,937 TWh to get 5300 TWh. The value 13,937 TWh is the Plan’s standard-demand load, 1591 GW-y, converted into TWh units by multiplying X 8760 hours /yr.
This calculation is valid only if the PV and CSP solar nameplate capacities in column 3 of rows 9 and 10 of Table 2 really do succeed in raising their capacity factor higher than 21.9%, which was their actual performance in 2015.
To the extent that they are unable to do so, those rows will be stuck providing utility-solar energy at their present CF level, which would be 2,553,300 MWp-ac X 8760 hr /y X 21.9% CF = 4070 TWh of electric energy in 2050 for the whole USA.
To the extent the lower 21.9% capacity factor prevails, the percentage of utility solar that must be allocated to these northern 8 states must approach closer to 42%, not just 32%. [1709 TWh (8 states in 2050) ÷ 4070 TWh (USA in 2050) = 0.420 or 42%]
13. http://apps2.eere.energy.gov/wind/windexchange/wind_installed_capacity.asp (interactive: click spreadsheet or annual maps) Installed Wind Capacity, US annual to 2015
14. http://www.seia.org/research-resources/solar-industry-data
third bar graph - US solar annual installed
http://www.seia.org/news/us-solar-market-sets-new-record-installing-73-gw-solar-pv-2015
first bar graph Note that the bar graph is expressed in dc watts. Grid capacities are expressed in ac watts. For conversion, assume ac-to-dc inverter conversion efficiency = 0.85 (85%). 7.286 GWdc X 0.85 = 6.19 GWac
Alternatively
15. http://www.eia.gov/totalenergy/data/monthly/pdf/sec7_5.pdf
190,927 GW-h ÷ 8760 hr /yr = 21.8 GW-y
16. Ibid. 26,473 GW-h ÷ 8760 hr /yr = 3.0 GW-y
17. Ibid. 251,168 GW-h = 28.7 GW-y
18. Ibid. 1,335,068 GW-h = 152.4 GW-y
19. http://www.eia.gov/dnav/ng/ng_cons_sum_dcu_nus_a.htm
20. Ibid. (residential + commercial + industrial values)
21. http://apps2.eere.energy.gov/wind/windexchange/wind_installed_capacity.asp
Ibid. No. 13
22. http://www.nrel.gov/docs/fy13osti/56290.pdf
p. v, Table ES-1, Summary of Land-Use Requirements for PV and CSP Projects in the United States
Direct Area, Capacity-weighted average Land Use, Large PV
22.3 https://www.choice.com.au/home-improvement/energy-saving/solar/review-and-compare/solar-panels
choose Sunpower SPR-E20-327
STC Power Rating: 327 Wdc
PTC Power Rating: 301.4 W;
PTC derate factor = 0.922; 301.4 W ÷ 327 W = 0.922
STC Power per unit of area: 200.5 W /m2
so derated PTC Power per unit of area = 0.922 X 200.5 = 185 Wdc /m2
dc-to-ac conversion at 0.85 efficiency; 0.85 X 185 Wdc /m2 = 157 Wac /m2
Round to 160 Wac /m2 for discussion & estimation
22.5 Panels' nominal power ratings, which are greater than 160 W /m2, are expressed for Standard Test Conditions and refer to dc electric output, which is incompatible with society’s mostly ac electric loads. Devices such as induction motors, lights, coiled heating elements, transformer-operated power supplies for battery-chargers and consumer electronic devices.
In other words, there are at least three possible quantifications for photovoltaic surface power density. They are 1) STC-dc; 2) PTC-dc; and 3) PTC-ac. Only PTC-ac is useful for land area discussion.
In 2016 the best quality mass-production panel, when newly installed, has about 160 W /m2, rated PTC-ac. Age degradation occurs at rates from 0.25% to 1% per year. At the end of an assumed 40-year lifetime such a panel will have declined to 96 –144 W /m2.
22.7 Ibid. No. 22
p. 12, Sec. 4.2.1, Evaluation of PV Packing Factors;
p. 13, Figure 7, Capacity-weighted average packing factor for PV projects
22.8 The area between rows (panel edge to panel edge) is somewhat greater than 60,000 m2 because of the plumb trigonometry of the panels’ tilt angle.
23. For fixed mount: http://c.ymcdn.com/sites/www.aec.org/resource/resmgr/PDFs/WhitePaper_IBISAECAluminumSo.pdf
p. 6, Table 5, System Shipping Costs, Large Utility Ground Mount
Table 5 values are in English pounds, and refer to panel nominal (dc) kilowatts. Divide material value by 0.85 , dc /ac conversion efficiency, to relate to electric grid (ac) watts. For fixed-mount, 73 tonnes steel /MWp-ac:
6,835,683 pounds ÷ 50,000 kW = 137 pounds /kWac; 137 ÷ 2.204 pounds /kg =62 kg /kWdc = 62 tonnes steel /MWdc; divide 62 tonnes by 0.85 for 73 tonnes steel /MWac
For tracking-mount: https://us.sunpower.com/sites/sunpower/files/media-library/white-papers/wp-levelized-cost-drivers-electricity-utility-scale-photovoltaics.pdf
p. 14, Figure 12 Area Related Cost Components for a T20 Tracker Power Plant
Figure 12 values are in English tons, and refer to panel nominal (dc) kilowatts. Divide material values by 0.85 for ac. For tracking-mount, 88 tonnes steel /MWp-ac:
35,083 tons ÷ 423,191 kWdc = 0.0828 ton /kWdc; 0.0828 ton ÷ 1.102 tons /tonne = 0.0751 tonne /kWdc = 75.1 tonnes steel /MWdc; 75.1 t ÷ 0.85 = 88 tonnes steel /MWac
23.2. http://www.nrel.gov/docs/fy12osti/51664.pdf
p. 16-17
24. http://www.nrel.gov/docs/fy16osti/67142.pdf
p. 8, Overall Model Results, Utility Scale PV; 2016 fixed-tilt cost = $1.42 per dc watt. Divide by 0.83 for ac.
$1.42 /Wdc ÷ 0.83 = $1.71 /Wac (fixed-tilt in 2016)
{Our $1.71 /Wac contradicts the NREL study’s own Conclusion on p. 45, which states $1.99 /Wac for fixed-tilt utility farms. NREL’s conclusion was based on the assumption that fixed-tilt farms, unlike tracking-mount farms, would use “oversized” central inverter equipment, presumably only one inverter station instead of several, to convert the farm’s output into ac power with very poor conversion efficiency of 71%.
This was an arbitrary assumption, it seems to the author, since NREL felt free to assume non-“oversized” central inverter technology for tracking-mount farms. By doing so, achieving a more usual 83% conversion efficiency in the range that we have come to expect.
The author has reversed NREL’s “oversized” assumption for fixed-tilt farms’ inverter equipment. Now expecting 83% dc-to-ac conversion for both mounting types.}
25. Ibid.
p. 45, Conclusions (1);
$1.49 /Wdc ÷ 0.83 = $1.79 /Wac (single-axis tracking in 2016)
26. Ibid.
$1.42 for fixed-tilt and $1.49 for tracking-mount, per dc watt. Combined average $1.45 per dc watt.
p. 36, Utility Scale PV, Modeling Inputs;
Module Price:
$0.64 ÷ $1.42 = 45% for fixed mount
$0.64 ÷ $1.49 = 43% for tracking mount
44% average
Inverter Price:
$0.09 ÷ $1.42 = 6.3% for fixed mount
$0.10 ÷ $1.49 = 6.7% for tracking mount
6.5% average; round to 7%
Installation Labor:
http://www.nrel.gov/docs/fy15osti/64746.pdffor 2015 installations
See p.29, Figure 21
$0.16 /Wdc for fixed mount
$0.22 /Wdc for tracking mount
$0.19 /Wdc average labor cost in 2015
Labor cost declined by about one-third from 2015 to 2016. See NREL 2016 report. p. 8. Compare orange-color segments in the bar graphs for those two years. $0.19 declined to about $0.13 /Wdc.
$0.13 /Wdc ÷ $1.45 /Wdc = 9.0% for labor
27. Derivations of Table 2’s implied capacity factors for the three PV solar placements: utility-scale, residential roof, and commercial flat-roof:
Utility-Scale: In row 9’s PV utility, 30.73% X 1591 GW all-purpose load gives 488.9 GWavg, or 488.9 GW-y /year in energy units.
With nameplate capacity of “2,326,000 MW”, the Plan’s PV farms have energy potential of 2326 GW-y /year if the sun shined all the time.
Nameplate capacity values for utility-scale solar are almost always expressed in grid-compatible ac units. This nameplate capacity value ought to be written more explicitly as “2,326,000 MWp-ac”.
Implied CF = 488.9 GW-y ÷ 2326 GW-y = 21.0% implied.
Combined PV and CSP actual utility-solar CF in 2015 was 21.9%, as derived in footnote 12. Thus the Plan’s presumption for utility PV production in row 9 is reasonable. In fact, for mid- and long-term planning, if we could restrict utility solar farms to high insolation locations, especially our southwest, we could expect nationwide average PV solar capacity factor to rise into the mid-twenties. For example, recent performances by three large PV farms in Southern California, namely Solar Star, Topaz, and Desert Sunlight, show capacity factors ranging from 24.5% to 26.7%.
Residential: Nameplate capacities of residential rooftop solar are stated in dc power units, not ac units as for utility-scale projects. The value 379,500 MW in row 7 of Table 2 represents dc watt units. The 100% WWS Plan specifies dc watts in Table 4 on p. 8, and also acknowledges dc units in the final paragraph of Section 5.2 on p. 10.
Using the standard 85% dc /ac conversion efficiency for less dusty rooftop placement, this represents 0.85 X 379,500 = 322,575 MWp-ac, or 322.6 GWp-ac.
If the sun shined 100% of the time, the row 7 national residential equipment would have potential annual energy of 322.6 GW-y /year. In order to achieve actual annual energy of 63 GW-y, residential solar would require CF = 63 GW-y ÷ 322.6 GW-y = 19.5% implied.
That is an unreasonable expectation (objection) for a nationwide residential average, in this author’s opinion. It is probably impossible for nationwide residential solar CF to rise above its 2015 value of 14.4% derived in the Overview section. This is because of south-siting issues, many sloped roofs having unfavorable angle of tilt, and partial shading by trees and other buildings, as mentioned there.
Commercial flat-roof: Commercial rooftop solar, like residential, is specified in dc watt units, per Table 4 on p.8 of the 100% WWS Plan.
So row 8’s solar panel capacity of 276,500 MWp-dc converts to 0.85 X 276,500 MW = 235.0 GWp-ac, using 85% efficiency rule-of-thumb.
From column 4, “Percent of 2050 all-purpose load”, 3.24% X 1591 GW anticipates 51.5 GW-y /year. Implied capacity factor is given by CF = 51.5 GW-y ÷ 235.0 GW-y = 21.9%.
In high-insolation regions individual commercial rooftops can achieve capacity factors in the low- to mid-twenties range, comparable to ground-mount utility installations. But it is not plausible as a nationwide average, with most commercial facilities concentrated in low-insolation regions. 2015’s commercial rooftop solar CF of only 13.6% resulted in a shortfall of 19.5 GW-y, as derived in the Overview section. Therefore 51.5 GW-y annual energy production in row 8 is unreasonably optimistic.
28. http://www.nrel.gov/docs/fy16osti/67142.pdf
p. 8, Overall Model Results; all values are expressed in dc watts,
29. Ibid.
p. 25, Residential PV: Modeling Inputs and Assumptions;
module + string inverter + installation labor = $0.64 + $0.16 + $0.30 = $1.10. 22% + 6% + 10% = 38%
p. 8, bar graph; Scale orange segment for labor, 2.7 mm. Vertical scale factor = $0.11 per mm.
2.7 mm X $0.11 = $0.30 for labor
29.1. Ibid.
Inverter: 6%
Assume labor cost divides as 5% for panels and 5% for inverters.
One inverter replacement: 6% + 5% = 11%. Three additional replacements: 3 X 11% = 33%.
30. http://c.ymcdn.com/sites/www.aec.org/resource/resmgr/PDFs/WhitePaper_IBISAECAluminumSo.pdf
p. 6, Table 5, System Shipping Costs
Table 5 values are in English pounds, and refer to panel nominal (dc) kilowatts, compatible with the Plan’s Table 2, row 8.
28,000 pounds steel ÷ 80 kW = 350 pounds /kWdc; 350 pounds ÷ 2.204 pound /kg = 159 kg steel /kWdc
31. Ibid. No. 28
p. 8, Overall Model Results; commercial PV cost = $2.13 /Wdc
32. Ibid.
p. 31, Commercial PV: Modeling Inputs and Assumptions;
module + inverter + installation labor = $0.64 + $0.13 + $0.20 = $0.97 /Wdc. 30% + 6% + 10% = 46%
p. 8, bar graph; Scale orange segment for labor. 1.8 mm X $0.11 /mm = $0.20
32.1. Ibid. No. 29.5.
Same inverter parts and labor percentages for commercial rooftop: 6% (parts) + 5% (labor) = 11%.
Three additional inverter replacements: 3 X 11% = 33%.
32.5 www.nrel.gov/docs/fy15osti/64898.pdf
p.5, Average US PV System Prices over Time;
Vertical axis scale factor = $0.20 per mm (20 cents per mm)
Apply ruler scaling to the final three green boxes; measure their centers below the $2 grid line and apply 20 cents /mm scale factor.
For residential and commercial combined, use the final 3 gray boxes for 2016, 2017 and 2018. Ruler-scale the center of each box relative to the $2 grid line.
32.7 Ibid. No. 24
p.42, Model Application-Module Efficiency Inputs; blue data points (bottom curve);
Vertical axis scale factor = $0.035 per mm (3.5 cents /mm)
At today's (CA) 16.7% solar conversion efficiency (5 mm to the right of 15% on horizontal axis), project up and over to vertical axis; the intercept scales to $1.42 /Wdc.
Repeat for 25% on horizontal axis; vertical intercept scales to $1.32 /Wdc; divide by $1.42 /Wdc = 0.930, a reduction of 7%.
Repeat the procedure for commercial (yellow curve), and for residential (brown).
33. http://www.nrel.gov/docs/fy09osti/45834.pdf
p. 10, Table 1, Total Area, Average Area Requirements; expressed in hectare units (ha). 100 ha = 1 km2. 34.5 ha /MW = 0.345 km2 /MWp
34. http://www.windmatching.acroenergy.pl/turbine/227/
https://bravenewclimate.com/2009/10/18/tcase4/
Section 1. Wind turbines; daily material consumption based on 1160 wind turbines, model GE2.5xl.
335,000 t steel ÷ 1160 turbines = 289 t /turbine; 289 t /2.5 MW = 115.6 t steel /MWp
1,250,000 t concrete ÷ 1160 turbines = 1078 t /turbine; 1078 t /2.5 MW = 431 t concrete /MWp
35. Technical Report NREL/TP-500-40566, http://www.nrel.gov/wind/pdfs/40566.pdf
Regarding blade mass: p. 11, Figure 1, graphs of blade mass versus blade length (called rotor radius) show exponents between 2.5 and 2.9, as do formulas appearing in figure caption below;
Regarding blade cost: p. 12, Figure 2, cost graphs and figure caption formulas show exponents from 2.5 up to 3 (cubed power);
Regarding tower and foundation mass: p. 20, Figure 3, graph of total mass is proportional (straight-line, or linear) with product of swept area X height. Swept area and tower height tend to increase in tandem with design increases in turbine nameplate capacity So the proportional graph indicates an approximate cubed function verse rotor radius (horizontal-axis units are cubic meters).
36. https://www3.epa.gov/climatechange/ghgemissions/usinventoryreport.html
U.S. Greenhouse Gas Inventory Report: 1990-2014; Overview of Greenhouse Gases and Sources of Emissions, first paragraph
scroll to U.S. Greenhouse Gas Emissions by Economic Sector, 1990 - 2014
Sixth paragraph, $1710 /kW
lbl.gov is Lawrence Berkeley Lab, affiliate of US DOE and Univ. of California
38. Ibid.
Fifth paragraph
39. https://www.irena.org/documentdownloads/publications/re_technologies_cost_analysis-wind_power.pdf
p. 35, seventh paragraph
40. Correspondence thread with
Alfonso Alvaro
Corporate Director Strategy & Development
A division of JERANEAS COMPANY
Refurbish wind turbine
The $4.7 M cost is for a slightly larger turbine than the 2-MW unit quoted.
41. https://www.irena.org/documentdownloads/publications/re_technologies_cost_analysis-wind_power.pdf
p. 19, Table 4.1, Capital Investment Costs; Onshore : Offshore ratio = 1 : 2
42. http://www.aweo.org/windarea.html
From the list titled Areas of industrial wind facilities, the offshore wind farms have been extracted and are recorded here. On-line, the projects are listed alphabetically by location, first in the US (Delaware and Massachusetts). Then outside the USA (Br Col, Canada through UK) .
Winergy offshore, Del1,101 MW /67 mi2
Cape Wind (off shore), Mass.420 MW /24 mi2
Naikun Offshore, Hecate Strait, Br. Col.396 MW /100 km2
Horns Rev (off shore), Denmark160 MW /24 mi2
Horns Rev II (off shore), Denmark209 MW /35 mi2
Butendiek (off shore), Germany240 MW /35 km2
Duddon Sands (off shore), U.K.500 MW /66 km2
London Array (off shore)1,000 MW /245 km2
Walney (off shore), U.K.450 MW /74.5 km2
Average4.36 MW /km2 = 0.229 km2 /MW
43. https://en.wikipedia.org/wiki/Andasol_Solar_Power_Station
https://www.rwe.com/web/cms/mediablob/en/1115150/data/0/1/Further-information-about-Andasol.pdf
p. 8, Data about the Andasol power plants (Data per power plant); forecast gross electricity volume: about 180 GWh (X 3) = 540 GWh /yr
http://www.power-technology.com/projects/andasolsolarpower/ second paragraph; “The three units have a net electricity output of 150 GWh per annum from each plant. The third plant was commissioned in September 2011. Andasol 3 is expected to produce 165 million kilowatt hours of electricity every year.”
The author of the article contradicts himself in these contiguous sentences. The second sentence is the correct one; it is correct also regarding Andasol 1 and 2, since all three Andasol units are identical. 3 X 165 = 495 GWh /yr for entire Andasol.
44. https://www.rwe.com/web/cms/mediablob/en/1115150/data/0/1/Further-information-about-Andasol.pdf
page 8, Table labeled: Data about the Andasol power plants (Data per power plant); Terrain: approx 195 hectares (X 3) = 585 ha = 5.85 km2
45. From http://www.needs-project.org/docs/results/RS1a/RS1a%20D12.2%20Final%20report%20concentrating%20solar%20thermal%20power%20plants.pdf page 88,
referenced in https://bravenewclimate.com/2009/10/18/tcase4/
Section 2. Solar thermal. fifth paragraph
690,000 t steel / 680 MWavg X 56.5 MWavg (Andasol) = 57,300 tonnes steel used by Andasol
2,215,000 t concrete / 680 MWavg X 56.5 MWavg (Andasol) = 184,000 tonnes concrete used by Andasol
46. Ibid. No. 3, The 100% WWS Plan, Table S14, p. 91-92
Utility CSP w /storage:
Near-term values: 6148, 7535, 6000, 8500; average $7046 /kW
Future values: 5016, 3500, 6000; average $4839 /kW
47. http://www.power-technology.com/projects/andasolsolarpower/
first paragraph
https://en.wikipedia.org/wiki/Andasol_Solar_Power_Station
Description section, third paragraph
48. Ibid. No. 45
Utility PV fixed: Near-term and Future values: 1476, 2708, 1690, 3000, 1476, 2700, 1814, 1750; average $2077 /kWac
Utility PV tracking: Near-term and Future values: 3617, 1722, 2796, 3200, 3617, 1722, 2700, 3011, 2167, 1950, 3011; average $2683 /kWac
Assuming 50 /50 split between fixed-mount and tracking-mount in future, combining fixed average $2077 with tracking average $2683 gives overall average for utility PV solar = $2380 /kWac
Residential PV: Near-term and Future values: 4427,6351, 3740, 4500, 3443, 3127, 2100; average $3955 /kWdc
Commercial PV: Near-term and Future values: 2951, 5113, 2390, 3500, 2459, 2796, 1900; average $3016 /kWdc
49. The Plan’s authors explain the sources of the cost data that appear in Table S14 in a section titled ANNOTATION OF MAIN LITERATURE SOURCES USED IN OUR ANALYSIS OF THE NATIONAL-AVERAGE LCOE (TABLE S14), beginning on p. 107. (LCOE - Levelized Cost of Energy)
In the EIA (Energy information Administration) subsection the authors state that near-term [cost] estimates are from Table 8.2 of EIA (2014a). The Plan’s Table S14 near-term data entry is $3617 /kW, for tracking mount. No entry is present in the Plan’s table for fixed mount.
However, EIA’s Table 8.2 Cost and Performance Characteristics of New Central Station Electricity Generating Technologies in 2014 shows $3394 /kW for base overnight cost and $3564 /kW for total overnight cost (with no distinction between fixed and tracking mount). The Plan’s value $3617 /kW does not agree with EIA Table 8.2.
EIA appends a footnote pertaining to its assumed 150-MW capacity (utility-scale) that “Costs and capacities are expressed in terms of net AC power available to the grid for the installed capacity.” Meaning that costs are stated on an ac-watt basis, as is usual for utility-scale PV solar.
However, this ac-basis understanding is confounded in the subsection titled LBNL, Others on p. 109 [Lawrence Berkeley National Laboratory]. The Plan’s authors explicitly identify the data from the sources LBNL and others, at least, to state PV solar costs in per dc-watt units for all three placements, utility, commercial and residential; second and third paragraphs. This differs from the usual practice in non-academic publications, where utility-scale solar is described in ac-watt units.
So there is contradiction about the meaning of utility-scale PV solar costs in the Plan’s Table S14, as to whether the cost value refers to per dc-watt or per ac-watt units. We will follow our former practice of interpreting utility-scale values on an ac-watt basis. As usual, commercial and residential values are interpreted on a dc-watt basis.
50. Ibid. No. 45
From p. 92, Future wind
Onshore values: 1976, 1377, 2113; average $1822 /kWac
Offshore values: 5077, 3050, 3191; average $3773 /kWac
51. https://www.eia.gov/totalenergy/data/monthly/pdf/mer.pdf
U.S. Energy Information Administration / Monthly Energy Review, May 2016 , page 17, Table 1.7, Primary Energy Consumption; also p. 7, Table 1.3
52. http://www.eia.gov/totalenergy/data/monthly/pdf/sec7_5.pdf
Table 7.2a, for 2010:
hydro plus geo combined = 260,203 + 15,219 = 275,422 GW-h
Primary Energy (footnote 48) =97.48 Quads X 293.1e3 GW-h /Q = 28.6e6 GW-h PRI NRG;
275,422 GW-h ÷ 28.6e6 GW-h = 0.96%
53. Ibid.
For 2015: hydro plus geo combined = 251,168 + 16,767 = 267,935 GW-h
Primary Energy (Ibid. No. 48) = 97.527 Quads X 293.1e3 GW-h /Q = 28.6e6 GW-h PRI NRG (virtually no change from 2010)
267,935 GW-h ÷ 28.6e6 GW-h = 0.94%
54. Ibid.
hydro 2010: 260,203 GW-h; hydro 2015: 251,167 GW-h;
hydro has declined 3.5% in past 5 years
55. From FN 12, utility solar (PV + CSP) capacity = 13.76 GW; actual energy = 26,473 GW-h
From FN 12.3, residential capacity = 5.53 GW
From FN 12.4, residential actual energy = 6999 GW-h
From FN 12.5, commercial capacity = 6.00 GW
From FN 12.6, commercial (plus industrial) actual energy = 7140 GW-h
Total capacity, all 3 placements = 13.76 + 5.53 + 6.00 = 25.29 GW; potential = 25.29 GW X 8760 h =
221.5e12 W-h
Total actual energy = 26,473 + 6999 + 7140 = 40,612 GW-h
Overall solar capacity factor = Total actual energy ÷ potential = 40,612e9 W-h ÷ 221.5e12 W-h = 0.183 or 18.3%
56. Ibid. No. 12
57. http://energy.gov/sites/prod/files/2015/08/f25/2014-Wind-Technologies-Market-Report-8.7.pdf
page vii, Performance Trends section, first and second paragraphs
58. http://www.publicpurpose.com/freeway1.htm
section Cost of IHS on approximately p. 7; $329 B in 1996 dollars
http://stats.areppim.com/calc/calc_usdlrxdeflator.php
$329 B in 1996 dollars X 1.431 inflation = $471 B in 2015 dollars
59. http://web.stanford.edu/group/efmh/jacobson/Articles/I/CombiningRenew/CONUSGridIntegration.pdf
page 1
Ibid. No. 4
60. Ibid. No. 9
scroll to line 37065, year 2014
Alternatively
US nameplate & summer electric capacity - all sources code H37306 line 37065.xls
61. http://www.eia.gov/electricity/annual/html/epa_08_06_a.html
Most recent year 2012
62. http://www.westinghousenuclear.com/New-Plants/Small-Modular-Reactor
scroll to Westinghouse SMR features at a glance
http://www.energy.gov/ne/nuclear-reactor-technologies/small-modular-nuclear-reactors
first paragraph
63. https://bravenewclimate.com/2009/10/18/tcase4/
Section 3: Nuclear fission
Assumptions by Dr. Barry Brook about model AP1000: average power = 1154 MW X 91.5% CF = 1056 MWavg;
Building thesis is 680 MWavg per day. So 680 MWavg /day ÷ 1056 MWavg /reactor = 0.6439 reactor per day.
Steel use = 10,000 t /day. 10,000 t /day ÷ 0.6439 reactor /day = 15,500 t steel per reactor
Concrete use = 160,000 t /day. 160,000 t /day ÷ 0.6439 reactor /day = 248,000 t concrete per reactor
Footprint about 150 X 150 meters, Land area = 0.022 km2
AP1000-dimension footprint.pdf
http://me1065.wikidot.com/ap1000
see Comparison of Important Nuclear Island Buildings under fourth major section Simplification of Power Plant Design
scroll to any of several relevant drawings
fourth paragraph
twelfth paragraph
https://en.wikipedia.org/wiki/Changjiang_Nuclear_Power_Plant
Sidebar features
Section 2, South Korea tells a very different story; Scatter graph: Overnight construction cost in KRW currency = 2,000,000 KRW per kilowatt = $1740 /kW. One S. Korea KRW (Korean Won) = $0.000 87; so 2,000,000 KRW /kW above = $1740 / kW;
normalized to AP1000, 1120e6 W X $1740 /1e3 W = $1.9 billion /reactor
fourth paragraph
Two 1400-MW plants = 2800 MW total; $7 billion ÷ 2800 MW = $2.50 /W; $2.50 /W X 1120e6 W (AP1000) = $2.8 billion / reactor, a higher cost than indicated by scatter graph above.
Section: Nuclear power programme in the UAE, 9th paragraph, $20.4 billion cost
$25 billion cost:
https://en.wikipedia.org/wiki/APR-1400
Design section: Net electric power = 1400 MWe
66. Ibid. No. 3, 100% WWS Plan, https://web.stanford.edu/group/efmh/jacobson/Articles/I/USStatesWWS.pdf
p.91-92, Table S14; Nuclear, Advanced Pressurized Water Reactor - APWR: Near term and Future values: 5583, 6640, 6511, 4434, 4279, 6511, 3800, 6500; average $5532 /kW
67. https://aris.iaea.org/sites/..%5CPDF%5CAP1000.pdf
p. 4, Section 2.2, Reactor core and fuel design, third paragraph
http://www.westinghousenuclear.com/New-Plants/AP1000-PWR/Operations-and-Maintenance
first section: Improved Plant Performance
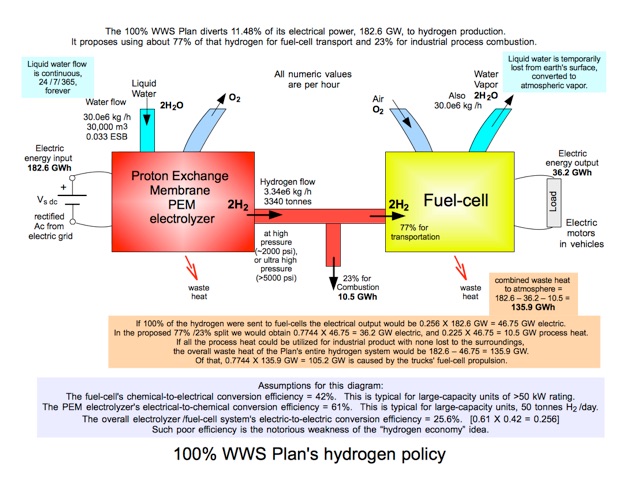
2016, June 22
Material Limits
Steel and concrete are the main construction materials required for the WWS buildout, but they are not limiting factors. There is enough of those two materials to complete the job. Not necessarily so for certain other materials.
We will set aside the issue of lanthanides, so-called rare earth metals. Their supply chains may occasionally become problematic because of their concentration in China and Brazil. But with the comparatively small quantities of them required for solar and wind equipment, existing world reserves are sufficient to carry humankind forward even if all countries were to adopt the 100% WWS idea.
Copper is another matter because we need so much of it. But the real problem is silver.
Material limits must be discussed only in the context of the entire world, not just the US. In principle, to deal with climate disruption the WWS Plan must be embraced by all mankind. In that spirit the Solutions Project does propose an individualized plan for every large country.
The overall global WWS Plan is presented at http://thesolutionsproject.org/resource/transition-chart-to-100-clean-renewable-energy/ . Download the first file, “Solutions-World-2015-Web”. It is helpful to print that S-curve graph.
Find the Solutions Project’s global total solar power and total wind power by referring to the values on the right-side vertical axis. Global average power is expected to be 11,797 GW. That is an average value, not a peak capacity.
As shown on the axis, solar is expected to provide 61.3% of the total, or 7230 GWavg. PV and CSP are combined.
Wind, onshore and offshore, is expected to provide 32.3% of 11,797 GW, or 3810 GWavg.
The Plan’s implied capacity factor for all PV solar in the US is about 21%.27 Extrapolating that CF to the entire world, global solar nameplate capacity must be 7230 GWavg ÷ 0.21 CF = 34,400 GWp-ac.
The Plan’s implied capacity factor for US onshore wind is 29%. For offshore it’s 39%.50.2 With more onshore than offshore, their weighted average CF is 33%. Extrapolating that CF to the entire world, global wind capacity must be 3810 GWavg ÷ 0.33 CF = 11,500 GWp, nameplate rating.
The industry-standard values for copper usage are:50.3
Solar PV: 5 tonnes Cu per megawatt of peak capacity. 5 tonnes /MWp
Wind: 3 t /MWp
These can be restated to be consistent with our preferred GW units as:
Solar PV: 5,000 tonnes Cu per gigawatt of peak capacity. 5,000 tonnes /GWp
Wind: 3,000 t /GWp
We subsume CSP construction into PV construction globally, justified by extrapolating the 84% /16% split between PV and CSP in the US Plan.
Therefore the copper required globally through 2050 solar construction would be 34,400 GWp X 5,000 t Cu /GWp = 172,000,000 tonnes Cu.
Required for global wind construction would be 11,500 GWp X 3,000 t Cu /GWp = 34,500,000 tonnes Cu.
Total = 172,000,000 + 34,500,000 = 206,500,000 tonnes of copper through year 2050, for solar & wind construction globally.
Worldwide proved reserves of copper are 720,000,000 tonnes. Go to https://minerals.usgs.gov/minerals/pubs/commodity/copper/mcs-2017-coppe.pdf
On Frame 2, page 55, refer to the table World Mine Production and Reserves. The units are thousands of tonnes. In Reserves column, World total = 720,000,000 t.
Therefore the global WWS build-out would consume 29% of the world’s proved copper reserves. [206,500,000 t ÷ 720,000,000 t = 29%]
Whether the various on-going industrial and electrical uses of copper could continue functioning under such an immense diversion from copper-mine output cannot now be known.
Silver
Mined silver supplies have not yet been stressed by solar equipment demand because humans have built so little solar to date. Worldwide, PV capacity was 303 GWp-ac at year-end 2016, and CSP was 4.8 GW, for a combined 308 GW.50.4 This is less than 1% of the Solutions Project’s 2050 goal of 34,400 GW, stated earlier.
Silver is an ingredient in the metal paste that forms the conducting fingers and busbars on the front surface of a photovoltaic cell. The silver content of crystalline silicon PV cells was about 31 milligrams per dc watt in 2016.50.5 This is a reduction from about 82 mg /Wdc in 2013, as solar manufacturers strive to minimize their silver consumption.
The photovoltaic industry projects a steady reduction going forward. It anticipates a goal of 13 mg /Wdc in 2026, the year when the world reaches the halfway point in total solar installation, per the Roadmap’s construction schedule.50.6 Therefore we can take 13 mg /W as the average silver usage rate for PV equipment over the 35-year plan duration, even if further reductions are achieved after 2026.
Extrapolating the US Roadmap’s 84% /16% split between PV and CSP, total global solar of 34,400 GWp-ac breaks down into 28,900 GWp-ac for PV and 5,500 GW for CSP.
The photovoltaic cells themselves must have dc power capacity greater than 28,900 GW, to allow for 85% conversion efficiency of the electronic inverters that convert dc to grid-compatible ac. The global Roadmap’s PV infrastructure must have dc capacity given by 28,900 ÷ 0.85 = 34,000 GWdc.
Therefore silver consumption for all global PV solar cells through 2050 can be estimated as 34,000 GWdc X 13 mg /Wdc = 442,000 tonnes.
CSP solar collector mirrors use silver for their reflective coating, applied 100-nanometers thick on steel parabolic bases. That requires 13 tonnes of silver per gigawatt of capacity.50.7 So for CSP, 5,500 GW X 13 t /GW = 72,000 additional tonnes of silver. Combined PV and CSP = 442,000 t + 72,000 t = 514,000 t.
The world’s proven silver reserves are 570,000 tonnes.50.8 The global Roadmap Plan would consume 90% of it.
Present non-solar industrial demand for silver is 15,700 tonnes annually.50.9 Even presuming no increase in global industrial demand despite the rapid industrialization of China, India and others, industrial consumption during the 35-year WWS buildout would be 35 yr X 15,700 t /yr = 550,000 t.
But only 56,000 tonnes of silver would remain in the ground after satisfying solar equipment usage of 514,000 t.
There isn’t enough silver on the planet to support the Solutions Project’s solar construction along with current industrial consumption.
Footnotes
50.2 https://web.stanford.edu/group/efmh/jacobson/Articles/I/USStatesWWS.pdf
The Solutions Project Roadmap Plan. See Frame 8, page 6, Table 2.
Onshore wind, row 1, column 3; 30.92% X 1591 GWavg = 492 GWavg. Column 4, Name-plate capacity = 1,701,000 MWp. CF = 492e9 Wavg ÷ 1,701,000e6 Wp = 0.289, or 29% onshore CF.
Offshore wind, row 2, column 3; 19.08% X 1591 GWavg = 304 GWavg. Column 4, Name-plate capacity = 780,900 MWp. CF = 304e9 Wavg ÷ 780,900e6 Wp = 0.389, or 39% offshore CF.
50.3
https://en.wikipedia.org/wiki/Copper_in_renewable_energy
Refer to the table “Copper usage in renewal energy generation”. Power values are expressed in terms of peak capacity.
Photovoltaics row, columns 2 and 4.
350 kilotonnes Cu ÷ 70 GWp cumulative installed PV solar = 350e3 tonnes ÷ 70e3 MWp = 5 tonnes Cu /MWp
Wind row, columns 2 and 4.
714 kilotonnes Cu ÷ 238 GWp cumulative installed wind = 3 tonnes Cu /MWp
50.4
See page 7.
https://en.wikipedia.org/wiki/Concentrated_solar_power#Deployment_around_the_world
See table Worldwide Concentrated Solar Power. 4.815 GWp in 2016.
50.5
http://www.itrpv.net/Reports/Downloads/2016/
Refer to Fig. 8 on page 11, Frame 13. The data point for 2016 indicates 95 milligrams of silver per cell (crystalline silicon technology). Assuming power rating of 3.1 watts per cell, the usage of silver is 95 mg ÷ 3.1 W = 31 mg /W.
The reference PV unit is SunPower Co. module E20-435, containing 128 cells. Module power rating = 401 Wdc under PTC (Photovoltaics for Utility-Scale Test Conditions, often referred to as Practical Test Conditions). 401 W ÷ 128 cells = 3.1 Wdc /cell.
It’s 435 W nominal rating refers to STC - Standard Test Conditions (laboratory).
http://www.iom3.org/sites/default/files/iom3-corp/Mason%20SMEET%202%20presentation%2027Feb13.pdf
See page 11, referring to February 2013. Silver price = $1.10 /gram. Silver cost per PV watt (PTC) = $0.09.
$0.09 /W ÷ $1.10 /g = 0.082 g /W or 82 mg /W.
50.6
Ibid. Footnote 50.5.
The data point for 2026 indicates 40 milligrams of silver per PV cell. 40 mg /cell ÷ 3.1 W /cell = 13 mg /W.
50.7
http://fossilhub.org/wp-content/uploads/2014/03/Pihl_etal2012_ConcSolarPower_materials.pdf
Material constraints for concentrating solar thermal power
See table 3 on page 5. 13 tonnes silver per GWac = 13e6 g /1e9 W = 13e–3 g /W = 13 mg /Wac
50.8
https://minerals.usgs.gov/minerals/pubs/commodity/silver/mcs-2017-silve.pdf
Refer to the first page. Units are tonnes. Reserves column, world total = 570,000 tonnes of silver
50.9
http://www.silverinstitute.org/wp-content/uploads/2017/08/SilverInterim2016.pdf
See page 5, row Industrial Fabrication, column year 2016. Units are millions of troy ounces (Moz). The conversion factor is 31.1 tonnes per Moz.
585 Moz X 31.1 t /Moz = 18,200 t /yr.
https://www.bullionvault.com/gold-news/silver-solar-011120173
See the first bar graph, year 2016. PV’s share is 14% X 18,200 t = 2,540 t.
18,200 t – 2,500 t = 15,700 t /yr.